Examples for Attractors.jl

Newton's fractal (basins of 2D map)

using Attractors
function newton_map(z, p, n)
    z1 = z[1] + im*z[2]
    dz1 = newton_f(z1, p[1])/newton_df(z1, p[1])
    z1 = z1 - dz1
    return SVector(real(z1), imag(z1))
end
newton_f(x, p) = x^p - 1
newton_df(x, p)= p*x^(p-1)

ds = DiscreteDynamicalSystem(newton_map, [0.1, 0.2], [3.0])
xg = yg = range(-1.5, 1.5; length = 400)
# Use non-sparse for using `basins_of_attraction`
mapper = AttractorsViaRecurrences(ds, (xg, yg);
    sparse = false, mx_chk_lost = 1000
)
basins, attractors = basins_of_attraction(mapper; show_progress = false)
basins

400×400 Matrix{Int32}:
 1  1  1  1  1  1  1  1  1  1  1  1  1  …  2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1  …  2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 ⋮              ⋮              ⋮        ⋱        ⋮              ⋮           
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3  …  3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3

attractors

Dict{Int32, StateSpaceSet{2, Float64}} with 3 entries:
  2 => 2-dimensional StateSpaceSet{Float64} with 1 points
  3 => 2-dimensional StateSpaceSet{Float64} with 1 points
  1 => 2-dimensional StateSpaceSet{Float64} with 1 points

Now let's plot this as a heatmap

using CairoMakie
# Set up some code for plotting attractors
function scatter_attractors!(ax, attractors)
    for k ∈ keys(attractors)
        x, y = columns(attractors[k])
        scatter!(ax, vec(attractors[k]);
            color = Cycled(k), markersize = 20,
            strokewidth = 3, strokecolor = :white
        )
    end
end

generate_cmap(n) = cgrad(Main.COLORS[1:n], n; categorical = true)
ids = sort!(unique(basins))
cmap = generate_cmap(length(ids))

fig, ax = heatmap(xg, yg, basins;
    colormap = cmap, colorrange = (ids[1] - 0.5, ids[end]+0.5),
)
scatter_attractors!(ax, attractors)
fig

We could get only the fractions of the basins of attractions using basins_fractions, which is typically the more useful thing to do in a high dimensional system. In such cases it is also typically more useful to define a sampler that generates initial conditions on the fly instead of pre-defining some initial conditions (as is done in basins_of_attraction. This is simple to do:

grid = (xg, yg)
mapper = AttractorsViaRecurrences(ds, grid;
    sparse = false, mx_chk_lost = 1000
)

sampler, = statespace_sampler(;
    min_bounds = minimum.(grid), max_bounds = maximum.(grid)
)

basins = basins_fractions(mapper, sampler)

Dict{Int64, Float64} with 3 entries:
  2 => 0.33
  3 => 0.346
  1 => 0.324

in this case, to also get the attractors we simply extract them from the underlying storage of the mapper:

attractors = extract_attractors(mapper)

Dict{Int32, StateSpaceSet{2, Float64}} with 3 entries:
  2 => 2-dimensional StateSpaceSet{Float64} with 1 points
  3 => 2-dimensional StateSpaceSet{Float64} with 1 points
  1 => 2-dimensional StateSpaceSet{Float64} with 1 points

Fractality of 2D basins of the (4D) magnetic pendulum

In this section we will calculate the basins of attraction of the four-dimensional magnetic pendulum. We know that the attractors of this system are all individual fixed points on the (x, y) plane so we will only compute the basins there. We can also use this opportunity to highlight a different method, the AttractorsViaProximity which works when we already know where the attractors are. Furthermore we will also use a projected_integrator to project the 4D system onto a 2D plane, saving a lot of computational time!

Computing the basins

First we need to load in the magnetic pendulum from the predefined dynamical systems

using PredefinedDynamicalSystems
ds = Systems.magnetic_pendulum(d=0.2, α=0.2, ω=0.8, N=3)

4-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      false
 dynamic rule:  MagneticPendulum
 ODE solver:    Tsit5
 ODE kwargs:    (abstol = 1.0e-6, reltol = 1.0e-6)
 parameters:    PredefinedDynamicalSystems.MagneticPendulumParams([1.0, 1.0, 1.0], 0.2, 0.2, 0.8)
 time:          0.0
 state:         [0.7094575840693688, 0.704748136859158, 0.0, 0.0]

Then, we create a projected system on the x-y plane

psys = ProjectedDynamicalSystem(ds, [1, 2], [0.0, 0.0])

2-dimensional ProjectedDynamicalSystem
 deterministic:  true
 discrete time:  false
 in-place:       false
 dynamic rule:   MagneticPendulum
 projection:     [1, 2]
 complete state: [0.0, 0.0]
 parameters:     PredefinedDynamicalSystems.MagneticPendulumParams([1.0, 1.0, 1.0], 0.2, 0.2, 0.8)
 time:           0.0
 state:          [0.7094575840693688, 0.704748136859158]

For this systems we know the attractors are close to the magnet positions, so we can just do

attractors = Dict(i => StateSpaceSet([dynamic_rule(ds).magnets[i]]) for i in 1:3)

Dict{Int64, StateSpaceSet{2, Float64}} with 3 entries:
  2 => 2-dimensional StateSpaceSet{Float64} with 1 points
  3 => 2-dimensional StateSpaceSet{Float64} with 1 points
  1 => 2-dimensional StateSpaceSet{Float64} with 1 points

and then create a

mapper = AttractorsViaProximity(psys, attractors)

AttractorsViaProximity
 rule f:      AttractorsViaProximity
 type:        ProjectedDynamicalSystem
 ε:           0.8660254037844386
 Δt:          1
 Ttr:         100
 attractors:  Dict{Int64, StateSpaceSet{2, Float64}} with 3 entries:
                2 => 2-dimensional StateSpaceSet{Float64} with 1 points
                3 => 2-dimensional StateSpaceSet{Float64} with 1 points
                1 => 2-dimensional StateSpaceSet{Float64} with 1 points

and as before, get the basins of attraction

xg = yg = range(-4, 4; length = 101)
grid = (xg, yg)
basins, = basins_of_attraction(mapper, grid; show_progress = false)
ids = sort!(unique(basins))
cmap = generate_cmap(length(ids))
fig, ax = heatmap(xg, yg, basins;
    colormap = cmap, colorrange = (ids[1] - 0.5, ids[end]+0.5),
)
scatter_attractors!(ax, attractors)
fig

Computing the uncertainty exponent

Let's now calculate the uncertainty_exponent for this system as well. The calculation is straightforward:

ε, f_ε, α = uncertainty_exponent(basins)
fig, ax = lines(log.(ε), log.(f_ε))
ax.title = "α = $(round(α; digits=3))"
fig

The actual uncertainty exponent is the slope of the curve (α) and indeed we get an exponent near 0 as we know a-priory the basins have fractal boundaries for the magnetic pendulum.

Computing the tipping probabilities

We will compute the tipping probabilities using the magnetic pendulum's example as the "before" state. For the "after" state we will change the γ parameter of the third magnet to be so small, its basin of attraction will virtually disappear. As we don't know when the basin of the third magnet will disappear, we switch the attractor finding algorithm back to AttractorsViaRecurrences.

ds = Systems.magnetic_pendulum(d=0.2, α=0.2, ω=0.8, N=3, γs = [1.0, 1.0, 0.1])
psys = ProjectedDynamicalSystem(ds, [1, 2], [0.0, 0.0])
mapper = AttractorsViaRecurrences(psys, (xg, yg); Δt = 1)
basins_after, attractors_after = basins_of_attraction(
    mapper, (xg, yg); show_progress = false
)
# matching attractors is important!
match_attractor_ids!(attractors_after, attractors)

# now plot
ids = sort!(unique(basins_after))
cmap = generate_cmap(length(ids))
fig, ax = heatmap(xg, yg, basins_after;
    colormap = cmap, colorrange = (ids[1] - 0.5, ids[end]+0.5),
)
scatter_attractors!(ax, attractors_after)
fig

P = tipping_probabilities(basins, basins_after)

3×2 Matrix{Float64}:
 0.505987  0.494013
 0.452071  0.547929
 0.547684  0.452316

As you can see P has size 3×2, as after the change only 2 attractors have been identified in the system (3 still exist but our state space discretization isn't fine enough to find the 3rd because it has such a small basin). Also, the first row of P is 50% probability to each other magnet, as it should be due to the system's symmetry.

3D basins via recurrences

To showcase the true power of AttractorsViaRecurrences we need to use a system whose attractors span higher-dimensional space. An example is

ds = Systems.thomas_cyclical(b = 0.1665)

3-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      false
 dynamic rule:  thomas_rule
 ODE solver:    Tsit5
 ODE kwargs:    (abstol = 1.0e-6, reltol = 1.0e-6)
 parameters:    [0.1665]
 time:          0.0
 state:         [1.0, 0.0, 0.0]

which, for this parameter, contains 5 coexisting attractors. 3 of them are entangled periodic orbits that span across all three dimensions, and the remaining 2 are fixed points.

To compute the basins we define a three-dimensional grid and call on it basins_of_attraction.

# This computation takes about an hour
xg = yg = zg = range(-6.0, 6.0; length = 251)
mapper = AttractorsViaRecurrences(ds, (xg, yg, zg))
basins, attractors = basins_of_attraction(mapper)
attractors

Dict{Int16, StateSpaceSet{3, Float64}} with 5 entries:
  5 => 3-dimensional StateSpaceSet{Float64} with 1 points
  4 => 3-dimensional StateSpaceSet{Float64} with 379 points
  6 => 3-dimensional StateSpaceSet{Float64} with 1 points
  2 => 3-dimensional StateSpaceSet{Float64} with 538 points
  3 => 3-dimensional StateSpaceSet{Float64} with 537 points
  1 => 3-dimensional StateSpaceSet{Float64} with 1 points

The basins of attraction are very complicated. We can try to visualize them by animating the 2D slices at each z value, to obtain:

Then, we visualize the attractors to obtain:

In the animation above, the scattered points are the attractor values the function AttractorsViaRecurrences found by itself. Of course, for the periodic orbits these points are incomplete. Once the function's logic understood we are on an attractor, it stops computing. However, we also simulated lines, by evolving initial conditions colored appropriately with the basins output.

The animation was produced with the code:

using GLMakie
fig = Figure()
display(fig)
ax = fig[1,1] = Axis3(fig; title = "found attractors")
cmap = cgrad(:dense, 6; categorical = true)

for i in keys(attractors)
    tr = attractors[i]
    markersize = length(attractors[i]) > 10 ? 2000 : 6000
    marker = length(attractors[i]) > 10 ? :circle : :rect
    scatter!(ax, columns(tr)...; markersize, marker, transparency = true, color = cmap[i])
    j = findfirst(isequal(i), bsn)
    x = xg[j[1]]
    y = yg[j[2]]
    z = zg[j[3]]
    tr = trajectory(ds, 100, SVector(x,y,z); Ttr = 100)
    lines!(ax, columns(tr)...; linewidth = 1.0, color = cmap[i])
end

a = range(0, 2π; length = 200) .+ π/4

record(fig, "cyclical_attractors.mp4", 1:length(a)) do i
    ax.azimuth = a[i]
end

Basin fractions continuation in the magnetic pendulum

Perhaps the simplest application of continuation is to produce a plot of how the fractions of attractors change as we continuously change the parameter we changed above to calculate tipping probabilities.

Computing the fractions

This is what the following code does:

# initialize projected magnetic pendulum
using Attractors, PredefinedDynamicalSystems
using Random: Xoshiro
ds = Systems.magnetic_pendulum(; d = 0.3, α = 0.2, ω = 0.5)
xg = yg = range(-3, 3; length = 101)
ds = ProjectedDynamicalSystem(ds, 1:2, [0.0, 0.0])
# Choose a mapper via recurrences
mapper = AttractorsViaRecurrences(ds, (xg, yg); Δt = 1.0)
# What parameter to change, over what range
γγ = range(1, 0; length = 101)
prange = [[1, 1, γ] for γ in γγ]
pidx = :γs
# important to make a sampler that respects the symmetry of the system
sampler, = statespace_sampler(Xoshiro(1234); spheredims = 2, radius = 3.0)
# continue attractors and basins:
# `Inf` threshold fits here, as attractors move smoothly in parameter space
rsc = RecurrencesSeededContinuation(mapper; threshold = Inf)
fractions_curves, attractors_info = continuation(
    rsc, prange, pidx, sampler;
    show_progress = false, samples_per_parameter = 100
)
# Show some characteristic fractions:
fractions_curves[[1, 50, 101]]

3-element Vector{Dict{Int64, Float64}}:
 Dict(2 => 0.3, 3 => 0.33, 1 => 0.37)
 Dict(2 => 0.21359223300970873, 3 => 0.47572815533980584, 1 => 0.3106796116504854)
 Dict(3 => 0.47058823529411764, 1 => 0.5294117647058824)

Plotting the fractions

We visualize them using a predefined function that you can find in docs/basins_plotting.jl

# careful; `prange` isn't a vector of reals!
Main.basins_curves_plot(fractions_curves, γγ)

"Bifurcation curves"

A by-product of the analysis is that we can obtain bifurcation curves for free. However, only the stable branches can be obtained!

fig = Figure()
ax = Axis(fig[1,1]; xlabel = L"\gamma_3", ylabel = "fixed point")
# choose how to go from attractor to real number representation
function real_number_repr(attractor)
    p = attractor[1]
    return (p[1] + p[2])/2
end

for (i, γ) in enumerate(γγ)
    for (k, attractor) in attractors_info[i]
        scatter!(ax, γ, real_number_repr(attractor); color = Cycled(k))
    end
end
fig

as you can see, two of the three fixed points, and their stability, do not depend at all on the parameter value, since this parameter value tunes the magnetic strength of only the third magnet. Nevertheless, the fractions of basin of attraction of all attractors depend strongly on the parameter. This is a simple example that highlights excellently how this new approach we propose here should be used even if one has already done a standard linearized bifurcation analysis.

Extinction of a species in a multistable competition model

In this advanced example we utilize both RecurrencesSeededContinuation and aggregate_attractor_fractions in analyzing species extinction in a dynamical model of competition between multiple species. The final goal is to show the percentage of how much of the state space leads to the extinction or not of a pre-determined species, as we vary a parameter. The model however displays extreme multistability, a feature we want to measure and preserve before aggregating information into "extinct or not".

To measure and preserve this we will apply RecurrencesSeededContinuation as-is first. Then we can aggregate information. First we have

using Attractors, OrdinaryDiffEq
using PredefinedDynamicalSystems
using Random: Xoshiro
# arguments to algorithms
samples_per_parameter = 1000
total_parameter_values = 101
diffeq = (alg = Vern9(), reltol = 1e-9, abstol = 1e-9, maxiters = Inf)
recurrences_kwargs = (; Δt= 1.0, mx_chk_fnd_att=9, diffeq);
# initialize dynamical syste and sampler
ds = PredefinedDynamicalSystems.multispecies_competition() # 8-dimensional
ds = CoupledODEs(ODEProblem(ds), diffeq)
# define grid in state space
xg = range(0, 60; length = 300)
grid = ntuple(x -> xg, 8)
prange = range(0.2, 0.3; length = total_parameter_values)
pidx = :D
sampler, = statespace_sampler(Xoshiro(1234);
    min_bounds = minimum.(grid), max_bounds = maximum.(grid)
)
# initialize mapper
mapper = AttractorsViaRecurrences(ds, grid; recurrences_kwargs...)
# perform continuation of attractors and their basins
continuation = RecurrencesSeededContinuation(mapper; threshold = Inf)
fractions_curves, attractors_info = continuation(
    continuation, prange, pidx, sampler;
    show_progress = true, samples_per_parameter
);
Main.basins_curves_plot(fractions_curves, prange; separatorwidth = 1)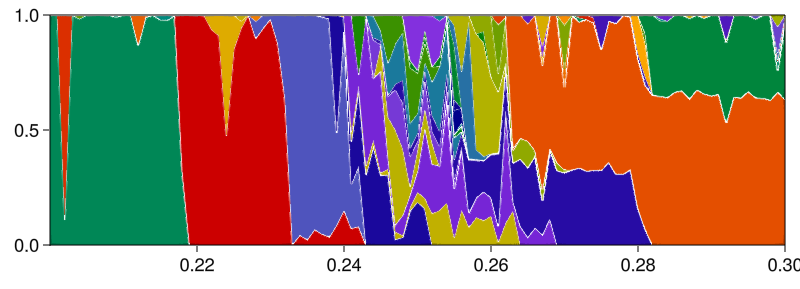

this example is not actually run when building the docs, because it takes about 60 minutes to complete depending on the computer; we load precomputed results instead

As you can see, the system has extreme multistability with 64 unique attractors (according to the default matching behavior in RecurrencesSeededContinuation; a stricter matching with less than Inf threshold would generate more "distinct" attractors). One could also isolate a specific parameter slice, and do the same as what we do in the Fractality of 2D basins of the (4D) magnetic pendulum example, to prove that the basin boundaries are fractal, thereby indeed confirming the paper title "Fundamental Unpredictability".

Regardless, we now want to continue our analysis to provide a figure similar to the above but only with two colors: fractions of attractors where a species is extinct or not. Here's how:

species = 3 # species we care about its existence

featurizer = (A) -> begin
    i = isextinct(A, species)
    return SVector(Int32(i))
end
isextinct(A, idx = unitidxs) = all(a -> a <= 1e-2, A[:, idx])

# `minneighbors = 1` is crucial for grouping single attractors
groupingconfig = GroupViaClustering(; min_neighbors=1, optimal_radius_method=0.5)

aggregated_fractions, aggregated_info = aggregate_attractor_fractions(
    fractions_curves, attractors_info, featurizer, groupingconfig
)

Main.basins_curves_plot(aggregated_fractions, prange;
    separatorwidth = 1, colors = ["green", "black"],
    labels = Dict(1 => "extinct", 2 => "alive"),
)

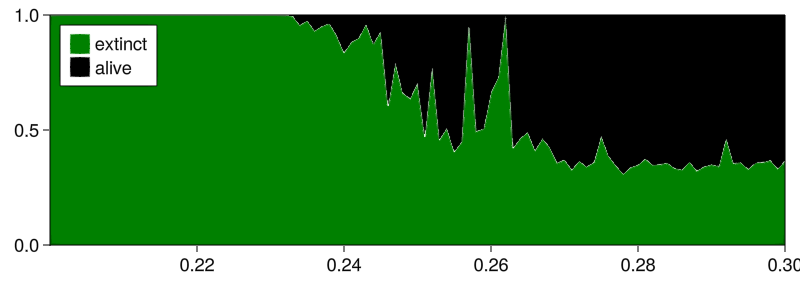
(in hindsight, the labels are reversed; attractor 1 is the alive one, but oh well)

Trivial featurizing and grouping for basins fractions

This is a rather trivial example showcasing the usage of AttractorsViaFeaturizing. Let us use once again the magnetic pendulum example. For it, we have a really good idea of what features will uniquely describe each attractor: the last points of a trajectory (which should be very close to the magnetic the trajectory converged to). To provide this information to the AttractorsviaFeaturizing we just create a julia function that returns this last point

using Attractors
using PredefinedDynamicalSystems

ds = Systems.magnetic_pendulum(d=0.2, α=0.2, ω=0.8, N=3)
psys = ProjectedDynamicalSystem(ds, [1, 2], [0.0, 0.0])

function featurizer(X, t)
    return X[end]
end

mapper = AttractorsViaFeaturizing(psys, featurizer; Ttr = 200, T = 1)

xg = yg = range(-4, 4; length = 101)

sampler, = statespace_sampler(; min_bounds = [-4,-4], max_bounds=[4,4])

fs = basins_fractions(mapper, sampler; show_progress = false)

Dict{Int64, Float64} with 3 entries:
  2 => 0.347
  3 => 0.315
  1 => 0.338

As expected, the fractions are each about 1/3 due to the system symmetry.

Featurizing and grouping across parameters (MCBB)

Here we showcase the example of the Monte Carlo Basin Bifurcation publication. For this, we will use GroupAcrossParametersContinuation while also providing a par_weight = 1 keyword. However, we will not use a network of 2nd order Kuramoto oscillators (as done in the paper by Gelbrecht et al.) because it is too costly to run on CI. Instead, we will use the Henon map and try to group attractors into period 1 (fixed point), period 3, and divergence to infinity. We will also use a pre-determined optimal radius for clustering, as we know a-priory the expected distances of features in feature space (due to the contrived form of the featurizer function below).

using Attractors, Random

b, a = -0.9, 1.4 # notice the non-default parameters
henon_rule(x, p, n) = SVector{2}(1.0 - p[1]*x[1]^2 + x[2], p[2]*x[1])
henon = DeterministicIteratedMap(henon_rule, zeros(2), [a,b])

function featurizer(a, t) # feature based on period!
    tol = 1e-5
    if abs(a[end-1,1] - a[end,1]) < tol
        # period 1
        return [1]
    elseif abs(a[end-3,1] - a[end,1]) < tol
        # period 3
        return [3]
    else
        return [100]
    end
end

henon

2-dimensional DeterministicIteratedMap
 deterministic: true
 discrete time: true
 in-place:      false
 dynamic rule:  henon_rule
 parameters:    [1.4, -0.9]
 time:          0
 state:         [0.0, 0.0]

clusterspecs = GroupViaClustering(optimal_radius_method = 1.0)
mapper = AttractorsViaFeaturizing(
    henon, featurizer, clusterspecs;
    T = 6, threaded = true, Ttr = 500,
)

continuation = GroupAcrossParameterContinuation(mapper; par_weight = 1.0)

ps = range(0.6, 1.1; length = 11)
pidx = 1
sampler, = statespace_sampler(Random.MersenneTwister(1234);
    min_bounds = [-2,-2], max_bounds = [2,2]
)

fractions_curves, clusters_info = Attractors.continuation(
    continuation, ps, pidx, sampler;
    samples_per_parameter = 100, show_progress = false
)
fractions_curves

Looking at the information of the "attractions" (here the clusters of the grouping procedure) makes it clear which label corresponds to which kind of attractor (fixed point, period 3, or divergence to infinity):

clusters_info

Using histograms and histogram distances as features

One of the aspects discussed in the original MCBB paper and implementation was the usage of histograms of the means of the variables of a dynamical system as the feature vector. This is useful in very high dimensional systems, such as oscillator networks, where the histogram of the means is significantly different in synchronized or unsychronized states.

This is possible to do with current interface without any modifications, by using two more packages: ComplexityMeasures.jl to compute histograms, and Distances.jl for the Kullback-Leibler divergence (or any other measure of distance in the space of probability distributions you fancy).

The only code we need to write to achieve this feature is a custom featurizer and providing an alternative distance to GroupViaClustering. The code would look like this:

using Distances: KLDivergence
using ComplexityMeasures: ValueHistogram, FixedRectangularBinning, probabilities

# you decide the binning for the histogram, but for a valid estimation of
# distances, all histograms must have exactly the same bins, and hence be
# computed with fixed ranges, i.e., using the `FixedRectangularBinning`
const binning = FixedRectangularBinning(range(-5, 5; length = 11))

function histogram_featurizer(A, t)
    ms = mean.(columns(A)) # vector of mean of each variable
    p = probabilities(ValueHistogram(binning), ms) # this is the histogram
    return vec(p) # because Distances.jl doesn't know `Probabilities`
end

gconfig = GroupViaClustering(;
    clust_distance_metric = KLDivergence(), # or any other PDF distance
)

You can then pass the histogram_featurizer and gconfig to an AttractorsViaFeaturizing and use the rest of the library as usual.