GitHub

Examples for Attractors.jl

Note that the examples utilize some convenience plotting functions offered by Attractors.jl which come into scope when using Makie (or any of its backends such as CairoMakie), see the visualization utilities for more.

Newton's fractal (basins of a 2D map)

using Attractors
function newton_map(z, p, n)
    z1 = z[1] + im*z[2]
    dz1 = newton_f(z1, p[1])/newton_df(z1, p[1])
    z1 = z1 - dz1
    return SVector(real(z1), imag(z1))
end
newton_f(x, p) = x^p - 1
newton_df(x, p)= p*x^(p-1)

ds = DiscreteDynamicalSystem(newton_map, [0.1, 0.2], [3.0])
xg = yg = range(-1.5, 1.5; length = 400)
grid = (xg, yg)
# Use non-sparse for using `basins_of_attraction`
mapper_newton = AttractorsViaRecurrences(ds, grid;
    sparse = false, consecutive_lost_steps = 1000
)
basins, attractors = basins_of_attraction(mapper_newton; show_progress = false)
basins
400×400 Matrix{Int64}:
 1  1  1  1  1  1  1  1  1  1  1  1  1  …  2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1  …  2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1  1     2  2  2  2  2  2  2  2  2  2  2  2
 ⋮              ⋮              ⋮        ⋱        ⋮              ⋮           
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3  …  3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3  3     3  3  3  3  3  3  3  3  3  3  3  3
attractors
Dict{Int64, StateSpaceSet{2, Float64, SVector{2, Float64}}} with 3 entries:
  2 => 2-dimensional StateSpaceSet{Float64} with 1 points
  3 => 2-dimensional StateSpaceSet{Float64} with 1 points
  1 => 2-dimensional StateSpaceSet{Float64} with 1 points

Now let's plot this as a heatmap, and on top of the heatmap, let's scatter plot the attractors. We do this in one step by utilizing one of the pre-defined plotting functions offered by Attractors.jl

using CairoMakie
fig = heatmap_basins_attractors(grid, basins, attractors)
Example block output

Instead of computing the full basins, we could get only the fractions of the basins of attractions using basins_fractions, which is typically the more useful thing to do in a high dimensional system. In such cases it is also typically more useful to define a sampler that generates initial conditions on the fly instead of pre-defining some initial conditions (as is done in basins_of_attraction. This is simple to do:

sampler, = statespace_sampler(grid)

basins = basins_fractions(mapper_newton, sampler)
Dict{Int64, Float64} with 2 entries:
  0 => 0.348
  1 => 0.652

in this case, to also get the attractors we simply extract them from the underlying storage of the mapper:

attractors = extract_attractors(mapper_newton)
Dict{Int64, StateSpaceSet{2, Float64, SVector{2, Float64}}} with 3 entries:
  2 => 2-dimensional StateSpaceSet{Float64} with 1 points
  3 => 2-dimensional StateSpaceSet{Float64} with 1 points
  1 => 2-dimensional StateSpaceSet{Float64} with 1 points

Shading basins according to convergence time

Continuing from above, we can utilize the convergence_and_basins_of_attraction function, and the shaded_basins_heatmap plotting utility function, to shade the basins of attraction based on the convergence time, with lighter colors indicating faster convergence to the attractor.

mapper_newton = AttractorsViaRecurrences(ds, grid;
    sparse = false, consecutive_lost_steps = 1000
)

basins, attractors, iterations = convergence_and_basins_of_attraction(
    mapper_newton, grid; show_progress = false
)

shaded_basins_heatmap(grid, basins, attractors, iterations)
Example block output

Minimal Fatal Shock

Here we find the Minimal Fatal Shock (MFS, see minimal_fatal_shock) for the attractors (i.e., fixed points) of Newton's fractal

shocks = Dict()
algo_bb = Attractors.MFSBlackBoxOptim()
for atr in values(attractors)
    u0 = atr[1]
    shocks[u0] = minimal_fatal_shock(mapper_newton, u0, (-1.5,1.5), algo_bb)
end
shocks
Dict{Any, Any} with 3 entries:
  [-0.5, -0.866025] => [-0.13061, 0.60818]
  [1.0, 0.0]        => [-0.461393, -0.417203]
  [-0.5, 0.866025]  => [0.592005, -0.190975]

To visualize results we can make use of previously defined heatmap

ax =  content(fig[1,1])
for (atr, shock) in shocks
    lines!(ax, [atr, atr + shock]; color = :orange, linewidth = 3)
end
fig
Example block output

Fractality of 2D basins of the (4D) magnetic pendulum

In this section we will calculate the basins of attraction of the four-dimensional magnetic pendulum. We know that the attractors of this system are all individual fixed points on the (x, y) plane so we will only compute the basins there. We can also use this opportunity to highlight a different method, the AttractorsViaProximity which works when we already know where the attractors are. Furthermore we will also use a ProjectedDynamicalSystem to project the 4D system onto a 2D plane, saving a lot of computational time!

Computing the basins

First we need to load in the magnetic pendulum from the predefined dynamical systems library

using Attractors, CairoMakie
using PredefinedDynamicalSystems
ds = PredefinedDynamicalSystems.magnetic_pendulum(d=0.2, α=0.2, ω=0.8, N=3)
4-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      false
 dynamic rule:  MagneticPendulum
 ODE solver:    Tsit5
 ODE kwargs:    (abstol = 1.0e-6, reltol = 1.0e-6)
 parameters:    PredefinedDynamicalSystems.MagneticPendulumParams([1.0, 1.0, 1.0], 0.2, 0.2, 0.8)
 time:          0.0
 state:         [0.7094575840693688, 0.704748136859158, 0.0, 0.0]

Then, we create a projected system on the x-y plane

psys = ProjectedDynamicalSystem(ds, [1, 2], [0.0, 0.0])
2-dimensional ProjectedDynamicalSystem
 deterministic:  true
 discrete time:  false
 in-place:       false
 dynamic rule:   MagneticPendulum
 projection:     [1, 2]
 complete state: [0.0, 0.0]
 parameters:     PredefinedDynamicalSystems.MagneticPendulumParams([1.0, 1.0, 1.0], 0.2, 0.2, 0.8)
 time:           0.0
 state:          [0.7094575840693688, 0.704748136859158]

For this systems we know the attractors are close to the magnet positions. The positions can be obtained from the equations of the system, provided that one has seen the source code (not displayed here), like so:

attractors = Dict(i => StateSpaceSet([dynamic_rule(ds).magnets[i]]) for i in 1:3)
Dict{Int64, StateSpaceSet{2, Float64, SVector{2, Float64}}} with 3 entries:
  2 => 2-dimensional StateSpaceSet{Float64} with 1 points
  3 => 2-dimensional StateSpaceSet{Float64} with 1 points
  1 => 2-dimensional StateSpaceSet{Float64} with 1 points

and then create a

mapper = AttractorsViaProximity(psys, attractors)
AttractorsViaProximity
 system:      ProjectedDynamicalSystem
 ε:           0.8660254037844386
 Δt:          1
 Ttr:         100
 attractors:  Dict{Int64, StateSpaceSet{2, Float64, SVector{2, Float64}}} with 3 entries:
                2 => 2-dimensional StateSpaceSet{Float64} with 1 points
                3 => 2-dimensional StateSpaceSet{Float64} with 1 points
                1 => 2-dimensional StateSpaceSet{Float64} with 1 points

and as before, get the basins of attraction

xg = yg = range(-4, 4; length = 201)
grid = (xg, yg)
basins, = basins_of_attraction(mapper, grid; show_progress = false)

heatmap_basins_attractors(grid, basins, attractors)
Example block output

Computing the uncertainty exponent

Let's now calculate the uncertainty_exponent for this system as well. The calculation is straightforward:

using CairoMakie
ε, f_ε, α = uncertainty_exponent(basins)
fig, ax = lines(log.(ε), log.(f_ε))
ax.title = "α = $(round(α; digits=3))"
fig
Example block output

The actual uncertainty exponent is the slope of the curve (α) and indeed we get an exponent near 0 as we know a-priory the basins have fractal boundaries for the magnetic pendulum.

Computing the tipping probabilities

We will compute the tipping probabilities using the magnetic pendulum's example as the "before" state. For the "after" state we will change the γ parameter of the third magnet to be so small, its basin of attraction will virtually disappear. As we don't know when the basin of the third magnet will disappear, we switch the attractor finding algorithm back to AttractorsViaRecurrences.

set_parameter!(psys, :γs, [1.0, 1.0, 0.1])
mapper = AttractorsViaRecurrences(psys, (xg, yg); Δt = 1)
basins_after, attractors_after = basins_of_attraction(
    mapper, (xg, yg); show_progress = false
)
# matching attractors is important!
rmap = match_statespacesets!(attractors_after, attractors)
# Don't forget to update the labels of the basins as well!
replace!(basins_after, rmap...)

# now plot
heatmap_basins_attractors(grid, basins_after, attractors_after)
Example block output

And let's compute the tipping "probabilities":

P = tipping_probabilities(basins, basins_after)
3×2 Matrix{Float64}:
 0.503072  0.496928
 0.448694  0.551306
 0.551061  0.448939

As you can see P has size 3×2, as after the change only 2 attractors have been identified in the system (3 still exist but our state space discretization isn't fine enough to find the 3rd because it has such a small basin). Also, the first row of P is 50% probability to each other magnet, as it should be due to the system's symmetry.

3D basins via recurrences

To showcase the true power of AttractorsViaRecurrences we need to use a system whose attractors span higher-dimensional space. An example is

using Attractors
using PredefinedDynamicalSystems
ds = PredefinedDynamicalSystems.thomas_cyclical(b = 0.1665)
3-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      false
 dynamic rule:  thomas_rule
 ODE solver:    Tsit5
 ODE kwargs:    (abstol = 1.0e-6, reltol = 1.0e-6)
 parameters:    [0.1665]
 time:          0.0
 state:         [1.0, 0.0, 0.0]

which, for this parameter, contains 3 coexisting attractors which are entangled periodic orbits that span across all three dimensions.

To compute the basins we define a three-dimensional grid and call on it basins_of_attraction.

# This computation takes about an hour
xg = yg = zg = range(-6.0, 6.0; length = 251)
mapper = AttractorsViaRecurrences(ds, (xg, yg, zg); sparse = false)
basins, attractors = basins_of_attraction(mapper)
attractors
Dict{Int16, StateSpaceSet{3, Float64}} with 5 entries:
  5 => 3-dimensional StateSpaceSet{Float64} with 1 points
  4 => 3-dimensional StateSpaceSet{Float64} with 379 points
  6 => 3-dimensional StateSpaceSet{Float64} with 1 points
  2 => 3-dimensional StateSpaceSet{Float64} with 538 points
  3 => 3-dimensional StateSpaceSet{Float64} with 537 points
  1 => 3-dimensional StateSpaceSet{Float64} with 1 points

Note: the reason we have 6 attractors here is because the algorithm also finds 3 unstable fixed points and labels them as attractors. This happens because we have provided initial conditions on the grid xg, yg, zg that start exactly on the unstable fixed points, and hence stay there forever, and hence are perceived as attractors by the recurrence algorithm. As you will see in the video below, they don't have any basin fractions

The basins of attraction are very complicated. We can try to visualize them by animating the 2D slices at each z value, to obtain:

Then, we visualize the attractors to obtain:

In the animation above, the scattered points are the attractor values the function AttractorsViaRecurrences found by itself. Of course, for the periodic orbits these points are incomplete. Once the function's logic understood we are on an attractor, it stops computing. However, we also simulated lines, by evolving initial conditions colored appropriately with the basins output.

The animation was produced with the code:

using GLMakie
fig = Figure()
display(fig)
ax = fig[1,1] = Axis3(fig; title = "found attractors")
cmap = cgrad(:dense, 6; categorical = true)

for i in keys(attractors)
    tr = attractors[i]
    markersize = length(attractors[i]) > 10 ? 2000 : 6000
    marker = length(attractors[i]) > 10 ? :circle : :rect
    scatter!(ax, columns(tr)...; markersize, marker, transparency = true, color = cmap[i])
    j = findfirst(isequal(i), bsn)
    x = xg[j[1]]
    y = yg[j[2]]
    z = zg[j[3]]
    tr = trajectory(ds, 100, SVector(x,y,z); Ttr = 100)
    lines!(ax, columns(tr)...; linewidth = 1.0, color = cmap[i])
end

a = range(0, 2π; length = 200) .+ π/4

record(fig, "cyclical_attractors.mp4", 1:length(a)) do i
    ax.azimuth = a[i]
end

Basins of attraction of a Poincaré map

PoincareMap is just another discrete time dynamical system within the DynamicalSystems.jl ecosystem. With respect to Attractors.jl functionality, there is nothing special about Poincaré maps. You simply initialize one use it like any other type of system. Let's continue from the above example of the Thomas cyclical system

using Attractors
using PredefinedDynamicalSystems
ds = PredefinedDynamicalSystems.thomas_cyclical(b = 0.1665);
3-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      false
 dynamic rule:  thomas_rule
 ODE solver:    Tsit5
 ODE kwargs:    (abstol = 1.0e-6, reltol = 1.0e-6)
 parameters:    [0.1665]
 time:          0.0
 state:         [1.0, 0.0, 0.0]

The three limit cycles attractors we have above become fixed points in the Poincaré map (for appropriately chosen hyperplanes). Since we already know the 3D structure of the basins, we can see that an appropriately chosen hyperplane is just the plane z = 0. Hence, we define a Poincaré map on this plane:

plane = (3, 0.0)
pmap = PoincareMap(ds, plane)
3-dimensional PoincareMap
 deterministic: true
 discrete time: true
 in-place:      false
 dynamic rule:  thomas_rule
 hyperplane:    (3, 0.0)
 crossing time: 0.0
 parameters:    [0.1665]
 time:          0
 state:         [1.0, 0.0, 0.0]

We define the same grid as before, but now only we only use the x-y coordinates. This is because we can utilize the special reinit! method of the PoincareMap, that allows us to initialize a new state directly on the hyperplane (and then the remaining variable of the dynamical system takes its value from the hyperplane itself).

xg = yg = range(-6.0, 6.0; length = 250)
grid = (xg, yg)
mapper = AttractorsViaRecurrences(pmap, grid; sparse = false)
AttractorsViaRecurrences
 system:      PoincareMap
 grid:        (-6.0:0.04819277108433735:6.0, -6.0:0.04819277108433735:6.0)
 attractors:  Dict{Int64, StateSpaceSet{2, Float64, SVector{2, Float64}}}()

All that is left to do is to call basins_of_attraction:

basins, attractors = basins_of_attraction(mapper; show_progress = false);
([1 1 … 2 2; 1 1 … 2 2; … ; 2 2 … 1 1; 2 2 … 1 1], Dict{Int64, StateSpaceSet{2, Float64, SVector{2, Float64}}}(2 => 2-dimensional StateSpaceSet{Float64} with 1 points, 3 => 2-dimensional StateSpaceSet{Float64} with 5 points, 1 => 2-dimensional StateSpaceSet{Float64} with 1 points))
heatmap_basins_attractors(grid, basins, attractors)
Example block output

just like in the example above, there is a fourth attractor with 0 basin fraction. This is an unstable fixed point, and exists exactly because we provided a grid with the unstable fixed point exactly on this grid

Irregular grid for AttractorsViaRecurrences

It is possible to provide an irregularly spaced grid to AttractorsViaRecurrences. This can make algorithm performance better for continuous time systems where the state space flow has significantly different speed in some state space regions versus others.

In the following example the dynamical system has only one attractor: a limit cycle. However, near the origin (0, 0) the timescale of the dynamics becomes very slow. As the trajectory is stuck there for quite a while, the recurrences algorithm may identify this region as an "attractor" (incorrectly). The solutions vary and can be to increase drastically the max time checks for finding attractors, or making the grid much more fine. Alternatively, one can provide a grid that is only more fine near the origin and not fine elsewhere.

The example below highlights that for rather coarse settings of grid and convergence thresholds, using a grid that is finer near (0, 0) gives correct results:

using Attractors, CairoMakie

function predator_prey_fastslow(u, p, t)
    α, γ, ϵ, ν, h, K, m = p
    N, P = u
    du1 = α*N*(1 - N/K) - γ*N*P / (N+h)
    du2 = ϵ*(ν*γ*N*P/(N+h) - m*P)
    return SVector(du1, du2)
end
γ = 2.5
h = 1
ν = 0.5
m = 0.4
ϵ = 1.0
α = 0.8
K = 15
u0 = rand(2)
p0 = [α, γ, ϵ, ν, h, K, m]
ds = CoupledODEs(predator_prey_fastslow, u0, p0)

fig = Figure()
ax = Axis(fig[1,1])

# when pow > 1, the grid is finer close to zero
for pow in (1, 2)
    xg = yg = range(0, 18.0^(1/pow); length = 200).^pow
    mapper = AttractorsViaRecurrences(ds, (xg, yg);
        Dt = 0.1, sparse = true,
        consecutive_recurrences = 10, attractor_locate_steps = 10,
        maximum_iterations = 1000,
    )

    # Find attractor and its fraction (fraction is always 1 here)
    sampler, _ = statespace_sampler(HRectangle(zeros(2), fill(18.0, 2)), 42)
    fractions = basins_fractions(mapper, sampler; N = 100, show_progress = false)
    attractors = extract_attractors(mapper)
    scatter!(ax, vec(attractors[1]); markersize = 16/pow, label = "pow = $(pow)")
end

axislegend(ax)

fig
Example block output

Subdivision Based Grid for AttractorsViaRecurrences

To achieve even better results for this kind of problematic systems than with previuosly introduced Irregular Grids we provide a functionality to construct Subdivision Based Grids in which one can obtain more coarse or dense structure not only along some axis but for a specific regions where the state space flow has significantly different speed. subdivision_based_grid enables automatic evaluation of velocity vectors for regions of originally user specified grid to further treat those areas as having more dense or coarse structure than others.

using Attractors, CairoMakie

function predator_prey_fastslow(u, p, t)
    α, γ, ϵ, ν, h, K, m = p
    N, P = u
    du1 = α*N*(1 - N/K) - γ*N*P / (N+h)
    du2 = ϵ*(ν*γ*N*P/(N+h) - m*P)
return SVector(du1, du2)
end
γ = 2.5
h = 1
ν = 0.5
m = 0.4
ϵ = 1.0
α = 0.8
K = 15
u0 = rand(2)
p0 = [α, γ, ϵ, ν, h, K, m]
ds = CoupledODEs(predator_prey_fastslow, u0, p0)

xg = yg = range(0, 18, length = 30)
# Construct `Subdivision Based Grid`
grid = subdivision_based_grid(ds, (xg, yg))
grid.lvl_array
30×30 Matrix{Int64}:
 4  4  4  4  4  4  4  4  4  4  4  4  4  …  3  3  3  3  3  3  3  3  3  3  3  3
 4  4  4  4  4  4  4  4  3  3  3  3  3     2  2  2  2  2  2  2  2  2  2  1  1
 4  4  4  4  4  4  3  3  3  3  2  2  2     2  1  1  1  1  1  1  1  1  1  1  1
 4  4  4  4  4  3  3  3  3  2  2  2  2     1  1  1  1  1  1  1  1  1  1  1  1
 4  4  4  4  4  3  3  3  3  2  2  2  2     1  1  1  1  1  1  1  1  1  1  1  0
 4  4  4  4  4  3  3  3  2  2  2  2  2  …  1  1  1  1  1  1  1  1  1  1  0  0
 4  4  4  4  4  3  3  3  2  2  2  2  2     1  1  1  1  1  1  1  1  1  0  0  0
 4  4  4  4  4  3  3  3  2  2  2  2  2     1  1  1  1  1  1  1  1  0  0  0  0
 4  4  4  4  4  3  3  3  2  2  2  2  2     1  1  1  1  1  1  1  1  0  0  0  0
 4  4  4  4  4  3  3  3  2  2  2  2  2     1  1  1  1  1  1  1  0  0  0  0  0
 ⋮              ⋮              ⋮        ⋱        ⋮              ⋮           
 4  4  4  4  3  3  3  2  2  2  2  2  1     1  1  1  1  0  0  0  0  0  0  0  0
 4  4  4  4  3  3  2  2  2  2  2  1  1     1  1  1  1  0  0  0  0  0  0  0  0
 4  4  4  3  3  3  2  2  2  2  2  1  1     1  1  1  0  0  0  0  0  0  0  0  0
 4  4  4  3  3  3  2  2  2  2  2  1  1     1  1  1  0  0  0  0  0  0  0  0  0
 4  4  4  3  3  2  2  2  2  2  1  1  1  …  1  1  1  0  0  0  0  0  0  0  0  0
 4  4  3  3  3  2  2  2  2  2  1  1  1     1  1  0  0  0  0  0  0  0  0  0  0
 4  4  3  3  3  2  2  2  2  2  1  1  1     1  1  0  0  0  0  0  0  0  0  0  0
 4  4  3  3  2  2  2  2  2  1  1  1  1     1  0  0  0  0  0  0  0  0  0  0  0
 4  3  3  3  2  2  2  2  2  1  1  1  1     1  0  0  0  0  0  0  0  0  0  0  0

The constructed array corresponds to levels of discretization for specific regions of the grid as a powers of 2, meaning that if area index is assigned to be 3, for example, the algorithm will treat the region as one being 2^3 = 8 times more dense than originally user provided grid (xg, yg).

Now upon the construction of this structure, one can simply pass it into mapper function as usual.

fig = Figure()
ax = Axis(fig[1,1])
# passing SubdivisionBasedGrid into mapper
mapper = AttractorsViaRecurrences(ds, grid;
        Dt = 0.1, sparse = true,
        consecutive_recurrences = 10, attractor_locate_steps = 10,
        maximum_iterations = 1000,
    )

# Find attractor and its fraction (fraction is always 1 here)
sampler, _ = statespace_sampler(HRectangle(zeros(2), fill(18.0, 2)), 42)
fractions = basins_fractions(mapper, sampler; N = 100, show_progress = false)
attractors_SBD = extract_attractors(mapper)
scatter!(ax, vec(attractors_SBD[1]); label = "SubdivisionBasedGrid")


# to compare the results we also construct RegularGrid of same length here
xg = yg = range(0, 18, length = 30)
mapper = AttractorsViaRecurrences(ds, (xg, yg);
        Dt = 0.1, sparse = true,
        consecutive_recurrences = 10, attractor_locate_steps = 10,
        maximum_iterations = 1000,
    )

sampler, _ = statespace_sampler(HRectangle(zeros(2), fill(18.0, 2)), 42)
fractions = basins_fractions(mapper, sampler; N = 100, show_progress = false)
attractors_reg = extract_attractors(mapper)
scatter!(ax, vec(attractors_reg[1]); label = "RegularGrid")

axislegend(ax)
fig
Example block output

Basin fractions continuation in the magnetic pendulum

Perhaps the simplest application of global_continuation is to produce a plot of how the fractions of attractors change as we continuously change the parameter we changed above to calculate tipping probabilities.

Computing the fractions

This is what the following code does:

# initialize projected magnetic pendulum
using Attractors, PredefinedDynamicalSystems
using Random: Xoshiro
ds = Systems.magnetic_pendulum(; d = 0.3, α = 0.2, ω = 0.5)
xg = yg = range(-3, 3; length = 101)
ds = ProjectedDynamicalSystem(ds, 1:2, [0.0, 0.0])
# Choose a mapper via recurrences
mapper = AttractorsViaRecurrences(ds, (xg, yg); Δt = 1.0)
# What parameter to change, over what range
γγ = range(1, 0; length = 101)
prange = [[1, 1, γ] for γ in γγ]
pidx = :γs
# important to make a sampler that respects the symmetry of the system
region = HSphere(3.0, 2)
sampler, = statespace_sampler(region, 1234)
# continue attractors and basins:
# `Inf` threshold fits here, as attractors move smoothly in parameter space
rsc = RecurrencesFindAndMatch(mapper; threshold = Inf)
fractions_cont, attractors_cont = global_continuation(
    rsc, prange, pidx, sampler;
    show_progress = false, samples_per_parameter = 100
)
# Show some characteristic fractions:
fractions_cont[[1, 50, 101]]
3-element Vector{Dict{Int64, Float64}}:
 Dict(2 => 0.32, 3 => 0.3, 1 => 0.38)
 Dict(2 => 0.47572815533980584, 3 => 0.4174757281553398, 1 => 0.10679611650485436)
 Dict(2 => 0.39215686274509803, 3 => 0.6078431372549019)

Plotting the fractions

We visualize them using a predefined function that you can find in docs/basins_plotting.jl

# careful; `prange` isn't a vector of reals!
plot_basins_curves(fractions_cont, γγ)
Example block output

Fixed point curves

A by-product of the analysis is that we can obtain the curves of the position of fixed points for free. However, only the stable branches can be obtained!

using CairoMakie
fig = Figure()
ax = Axis(fig[1,1]; xlabel = L"\gamma_3", ylabel = "fixed point")
# choose how to go from attractor to real number representation
function real_number_repr(attractor)
    p = attractor[1]
    return (p[1] + p[2])/2
end

for (i, γ) in enumerate(γγ)
    for (k, attractor) in attractors_cont[i]
        scatter!(ax, γ, real_number_repr(attractor); color = Cycled(k))
    end
end
fig
Example block output

as you can see, two of the three fixed points, and their stability, do not depend at all on the parameter value, since this parameter value tunes the magnetic strength of only the third magnet. Nevertheless, the fractions of basin of attraction of all attractors depend strongly on the parameter. This is a simple example that highlights excellently how this new approach we propose here should be used even if one has already done a standard linearized bifurcation analysis.

Extinction of a species in a multistable competition model

In this advanced example we utilize both RecurrencesFindAndMatch and aggregate_attractor_fractions in analyzing species extinction in a dynamical model of competition between multiple species. The final goal is to show the percentage of how much of the state space leads to the extinction or not of a pre-determined species, as we vary a parameter. The model however displays extreme multistability, a feature we want to measure and preserve before aggregating information into "extinct or not".

To measure and preserve this we will apply RecurrencesFindAndMatch as-is first. Then we can aggregate information. First we have

using Attractors, OrdinaryDiffEq
using PredefinedDynamicalSystems
using Random: Xoshiro
# arguments to algorithms
samples_per_parameter = 1000
total_parameter_values = 101
diffeq = (alg = Vern9(), reltol = 1e-9, abstol = 1e-9, maxiters = Inf)
recurrences_kwargs = (; Δt= 1.0, consecutive_recurrences=9, diffeq);
# initialize dynamical system and sampler
ds = PredefinedDynamicalSystems.multispecies_competition() # 8-dimensional
ds = CoupledODEs(ODEProblem(ds), diffeq)
# define grid in state space
xg = range(0, 60; length = 300)
grid = ntuple(x -> xg, 8)
prange = range(0.2, 0.3; length = total_parameter_values)
pidx = :D
sampler, = statespace_sampler(grid, 1234)
# initialize mapper
mapper = AttractorsViaRecurrences(ds, grid; recurrences_kwargs...)
# perform continuation of attractors and their basins
alg = RecurrencesFindAndMatch(mapper; threshold = Inf)
fractions_cont, attractors_cont = global_continuation(
    alg, prange, pidx, sampler;
    show_progress = true, samples_per_parameter
)
plot_basins_curves(fractions_cont, prange; separatorwidth = 1)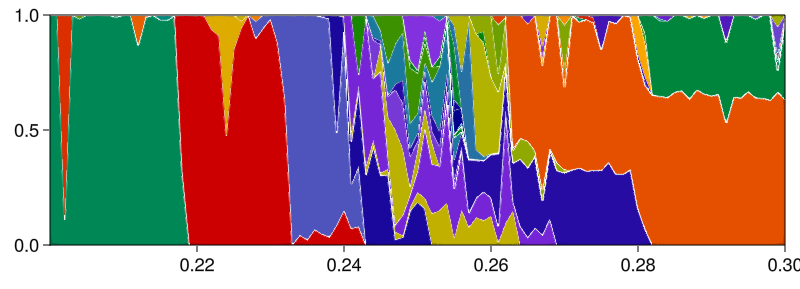

this example is not actually run when building the docs, because it takes about 60 minutes to complete depending on the computer; we load precomputed results instead

As you can see, the system has extreme multistability with 64 unique attractors (according to the default matching behavior in RecurrencesFindAndMatch; a stricter matching with less than Inf threshold would generate more "distinct" attractors). One could also isolate a specific parameter slice, and do the same as what we do in the Fractality of 2D basins of the (4D) magnetic pendulum example, to prove that the basin boundaries are fractal, thereby indeed confirming the paper title "Fundamental Unpredictability".

Regardless, we now want to continue our analysis to provide a figure similar to the above but only with two colors: fractions of attractors where a species is extinct or not. Here's how:

species = 3 # species we care about its existence

featurizer = (A) -> begin
    i = isextinct(A, species)
    return SVector(Int32(i))
end
isextinct(A, idx = unitidxs) = all(a -> a <= 1e-2, A[:, idx])

# `minneighbors = 1` is crucial for grouping single attractors
groupingconfig = GroupViaClustering(; min_neighbors=1, optimal_radius_method=0.5)

aggregated_fractions, aggregated_info = aggregate_attractor_fractions(
    fractions_cont, attractors_cont, featurizer, groupingconfig
)

plot_basins_curves(aggregated_fractions, prange;
    separatorwidth = 1, colors = ["green", "black"],
    labels = Dict(1 => "extinct", 2 => "alive"),
)

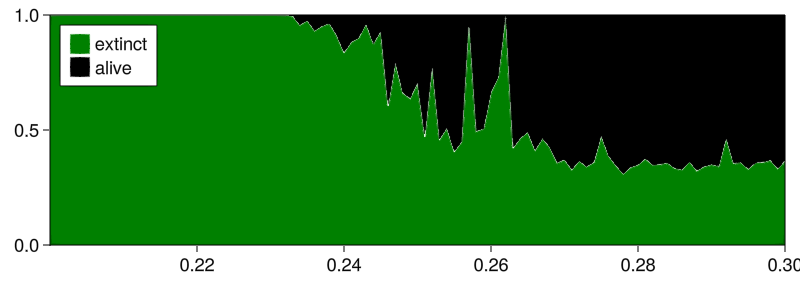
(in hindsight, the labels are reversed; attractor 1 is the alive one, but oh well)

Trivial featurizing and grouping for basins fractions

This is a rather trivial example showcasing the usage of AttractorsViaFeaturizing. Let us use once again the magnetic pendulum example. For it, we have a really good idea of what features will uniquely describe each attractor: the last points of a trajectory (which should be very close to the magnetic the trajectory converged to). To provide this information to the AttractorsViaFeaturizing we just create a julia function that returns this last point

using Attractors
using PredefinedDynamicalSystems

ds = Systems.magnetic_pendulum(d=0.2, α=0.2, ω=0.8, N=3)
psys = ProjectedDynamicalSystem(ds, [1, 2], [0.0, 0.0])

function featurizer(X, t)
    return X[end]
end

mapper = AttractorsViaFeaturizing(psys, featurizer; Ttr = 200, T = 1)

xg = yg = range(-4, 4; length = 101)

region = HRectangle([-4, 4], [4, 4])
sampler, = statespace_sampler(region)

fs = basins_fractions(mapper, sampler; show_progress = false)
Dict{Int64, Float64} with 3 entries:
  2 => 0.217
  3 => 0.4
  1 => 0.383

As expected, the fractions are each about 1/3 due to the system symmetry.

Featurizing and grouping across parameters (MCBB)

Here we showcase the example of the Monte Carlo Basin Bifurcation publication. For this, we will use FeaturizeGroupAcrossParameter while also providing a par_weight = 1 keyword. However, we will not use a network of 2nd order Kuramoto oscillators (as done in the paper by Gelbrecht et al.) because it is too costly to run on CI. Instead, we will use "dummy" system which we know analytically the attractors and how they behave versus a parameter.

the Henon map and try to group attractors into period 1 (fixed point), period 3, and divergence to infinity. We will also use a pre-determined optimal radius for clustering, as we know a-priory the expected distances of features in feature space (due to the contrived form of the featurizer function below).

using Attractors, Random

function dumb_map(dz, z, p, n)
    x, y = z
    r = p[1]
    if r < 0.5
        dz[1] = dz[2] = 0.0
    else
        if x > 0
            dz[1] = r
            dz[2] = r
        else
            dz[1] = -r
            dz[2] = -r
        end
    end
    return
end

r = 3.833
ds = DiscreteDynamicalSystem(dumb_map, [0., 0.], [r])
2-dimensional DeterministicIteratedMap
 deterministic: true
 discrete time: true
 in-place:      true
 dynamic rule:  dumb_map
 parameters:    [3.833]
 time:          0
 state:         [0.0, 0.0]

sampler, = statespace_sampler(HRectangle([-3.0, -3.0], [3.0, 3.0]), 1234)

rrange = range(0, 2; length = 21)
ridx = 1

featurizer(a, t) = a[end]
clusterspecs = GroupViaClustering(optimal_radius_method = "silhouettes", max_used_features = 200)
mapper = AttractorsViaFeaturizing(ds, featurizer, clusterspecs; T = 20, threaded = true)
gap = FeaturizeGroupAcrossParameter(mapper; par_weight = 1.0)
fractions_cont, clusters_info = global_continuation(
    gap, rrange, ridx, sampler; show_progress = false
)
fractions_cont
21-element Vector{Dict{Int64, Float64}}:
 Dict(1 => 1.0)
 Dict(2 => 1.0)
 Dict(3 => 1.0)
 Dict(4 => 1.0)
 Dict(5 => 1.0)
 Dict(6 => 0.47, 7 => 0.53)
 Dict(9 => 0.52, 8 => 0.48)
 Dict(11 => 0.44, 10 => 0.56)
 Dict(13 => 0.56, 12 => 0.44)
 Dict(15 => 0.46, 14 => 0.54)
 ⋮
 Dict(20 => 0.48, 21 => 0.52)
 Dict(22 => 0.54, 23 => 0.46)
 Dict(25 => 0.47, 24 => 0.53)
 Dict(27 => 0.6, 26 => 0.4)
 Dict(29 => 0.51, 28 => 0.49)
 Dict(31 => 0.49, 30 => 0.51)
 Dict(32 => 0.46, 33 => 0.54)
 Dict(34 => 0.45, 35 => 0.55)
 Dict(36 => 0.47, 37 => 0.53)

Looking at the information of the "attractors" (here the clusters of the grouping procedure) does not make it clear which label corresponds to which kind of attractor, but we can look at the:

clusters_info
21-element Vector{Dict{Int64, Vector{Float64}}}:
 Dict(1 => [0.0, 0.0])
 Dict(2 => [0.0, 0.0])
 Dict(3 => [0.0, 0.0])
 Dict(4 => [0.0, 0.0])
 Dict(5 => [0.0, 0.0])
 Dict(6 => [0.5, 0.5], 7 => [-0.5, -0.5])
 Dict(9 => [-0.6000000000000006, -0.6000000000000006], 8 => [0.6000000000000005, 0.6000000000000005])
 Dict(11 => [0.6999999999999995, 0.6999999999999995], 10 => [-0.7000000000000002, -0.7000000000000002])
 Dict(13 => [0.7999999999999995, 0.7999999999999995], 12 => [-0.8, -0.8])
 Dict(15 => [0.8999999999999992, 0.8999999999999992], 14 => [-0.8999999999999991, -0.8999999999999991])
 ⋮
 Dict(20 => [-1.200000000000001, -1.200000000000001], 21 => [1.2000000000000013, 1.2000000000000013])
 Dict(22 => [-1.2999999999999987, -1.2999999999999987], 23 => [1.299999999999999, 1.299999999999999])
 Dict(25 => [1.3999999999999992, 1.3999999999999992], 24 => [-1.4000000000000001, -1.4000000000000001])
 Dict(27 => [-1.5, -1.5], 26 => [1.5, 1.5])
 Dict(29 => [1.5999999999999994, 1.5999999999999994], 28 => [-1.5999999999999996, -1.5999999999999996])
 Dict(31 => [-1.7000000000000013, -1.7000000000000013], 30 => [1.7000000000000015, 1.7000000000000015])
 Dict(32 => [-1.7999999999999985, -1.7999999999999985], 33 => [1.7999999999999983, 1.7999999999999983])
 Dict(34 => [-1.9000000000000006, -1.9000000000000006], 35 => [1.9000000000000015, 1.9000000000000015])
 Dict(36 => [-2.0, -2.0], 37 => [2.0, 2.0])

Using histograms and histogram distances as features

One of the aspects discussed in the original MCBB paper and implementation was the usage of histograms of the means of the variables of a dynamical system as the feature vector. This is useful in very high dimensional systems, such as oscillator networks, where the histogram of the means is significantly different in synchronized or unsychronized states.

This is possible to do with current interface without any modifications, by using two more packages: ComplexityMeasures.jl to compute histograms, and Distances.jl for the Kullback-Leibler divergence (or any other measure of distance in the space of probability distributions you fancy).

The only code we need to write to achieve this feature is a custom featurizer and providing an alternative distance to GroupViaClustering. The code would look like this:

using Distances: KLDivergence
using ComplexityMeasures: ValueHistogram, FixedRectangularBinning, probabilities

# you decide the binning for the histogram, but for a valid estimation of
# distances, all histograms must have exactly the same bins, and hence be
# computed with fixed ranges, i.e., using the `FixedRectangularBinning`

function histogram_featurizer(A, t)
    binning = FixedRectangularBinning(range(-5, 5; length = 11))
    ms = mean.(columns(A)) # vector of mean of each variable
    p = probabilities(ValueHistogram(binning), ms) # this is the histogram
    return vec(p) # because Distances.jl doesn't know `Probabilities`
end

gconfig = GroupViaClustering(;
    clust_distance_metric = KLDivergence(), # or any other PDF distance
)

You can then pass the histogram_featurizer and gconfig to an AttractorsViaFeaturizing and use the rest of the library as usual.

Edge tracking

To showcase how to run the edgetracking algorithm, let us use it to find the saddle point of the bistable FitzHugh-Nagumo (FHN) model, a two-dimensional ODE system originally conceived to represent a spiking neuron. We define the system in the following form:

using OrdinaryDiffEq: Vern9

function fitzhugh_nagumo(u,p,t)
    x, y = u
    eps, beta = p
    dx = (x - x^3 - y)/eps
    dy = -beta*y + x
    return SVector{2}([dx, dy])
end

params = [0.1, 3.0]
ds = CoupledODEs(fitzhugh_nagumo, ones(2), params, diffeq=(;alg = Vern9(), reltol=1e-11))
2-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      false
 dynamic rule:  fitzhugh_nagumo
 ODE solver:    Vern9
 ODE kwargs:    (reltol = 1.0e-11,)
 parameters:    [0.1, 3.0]
 time:          0.0
 state:         [1.0, 1.0]

Now, we can use Attractors.jl to compute the fixed points and basins of attraction of the FHN model.

xg = yg = range(-1.5, 1.5; length = 201)
grid = (xg, yg)
mapper = AttractorsViaRecurrences(ds, grid; sparse=false)
basins, attractors = basins_of_attraction(mapper)
attractors
Dict{Int64, StateSpaceSet{2, Float64, SVector{2, Float64}}} with 3 entries:
  2 => 2-dimensional StateSpaceSet{Float64} with 1 points
  3 => 2-dimensional StateSpaceSet{Float64} with 1 points
  1 => 2-dimensional StateSpaceSet{Float64} with 1 points

The basins_of_attraction function found three fixed points: the two stable nodes of the system (labelled A and B) and the saddle point at the origin. The saddle is an unstable equilibrium and typically will not be found by basins_of_attraction. Coincidentally here we initialized an initial condition exactly on the saddle, and hence it was found. We can always find saddles with the edgetracking function. For illustration, let us initialize the algorithm from two initial conditions init1 and init2 (which must belong to different basins of attraction, see figure below).

attractors_AB = Dict(1 => attractors[1], 2 => attractors[2])
init1, init2 = [-1.0, -1.0], [-1.0, 0.2]
([-1.0, -1.0], [-1.0, 0.2])

Now, we run the edge tracking algorithm:

et = edgetracking(ds, attractors_AB; u1=init1, u2=init2,
    bisect_thresh = 1e-3, diverge_thresh = 2e-3, Δt = 1e-5, abstol = 1e-3
)

et.edge[end]
2-element SVector{2, Float64} with indices SOneTo(2):
  0.0012222453694255174
 -0.0008308993082805703

The algorithm has converged to the origin (up to the specified accuracy) where the saddle is located. The figure below shows how the algorithm has iteratively tracked along the basin boundary from the two initial conditions (red points) to the saddle (green square). Points of the edge track (orange) at which a re-bisection occured are marked with a white border. The figure also depicts two trajectories (blue) intialized on either side of the basin boundary at the first bisection point. We see that these trajectories follow the basin boundary for a while but then relax to either attractor before reaching the saddle. By counteracting the instability of the saddle, the edge tracking algorithm instead allows to track the basin boundary all the way to the saddle, or edge state.

traj1 = trajectory(ds, 2, et.track1[et.bisect_idx[1]], Δt=1e-5)
traj2 = trajectory(ds, 2, et.track2[et.bisect_idx[1]], Δt=1e-5)

fig = Figure()
ax = Axis(fig[1,1], xlabel="x", ylabel="y")
heatmap_basins_attractors!(ax, grid, basins, attractors, add_legend=false, labels=Dict(1=>"Attractor A", 2=>"Attractor B", 3=>"Saddle"))
lines!(ax, traj1[1][:,1], traj1[1][:,2], color=:dodgerblue, linewidth=2, label="Trajectories")
lines!(ax, traj2[1][:,1], traj2[1][:,2], color=:dodgerblue, linewidth=2)
lines!(ax, et.edge[:,1], et.edge[:,2], color=:orange, linestyle=:dash)
scatter!(ax, et.edge[et.bisect_idx,1], et.edge[et.bisect_idx,2], color=:white, markersize=15, marker=:circle)
scatter!(ax, et.edge[:,1], et.edge[:,2], color=:orange, markersize=11, marker=:circle, label="Edge track")
scatter!(ax, [-1.0,-1.0], [-1.0, 0.2], color=:red, markersize=15, label="Initial conditions")
xlims!(ax, -1.2, 1.1); ylims!(ax, -1.3, 0.8)
axislegend(ax, position=:rb)
fig
Example block output

In this simple two-dimensional model, we could of course have found the saddle directly by computing the zeroes of the ODE system. However, the edge tracking algorithm allows finding edge states also in high-dimensional and chaotic systems where a simple computation of unstable equilibria becomes infeasible.