Overarching tutorial for DynamicalSystems.jl

This page serves as a short but to-the-point introduction to the DynamicalSystems.jl library. It outlines the core components, and how they establish an interface that is used by the rest of the library. It also provides a couple of usage examples to connect the various packages of the library together.

Going through this tutorial should take you about 20 minutes.

Installation

To install DynamicalSystems.jl, simply do:

using Pkg; Pkg.add("DynamicalSystems")

This installs several packages for the Julia language. These are the sub-modules/packages that comprise DynamicalSystems.jl, see contents for more. All of the functionality is brought into scope when doing:

using DynamicalSystems

in your Julia session.

Package versions used

import Pkg

Pkg.status(["DynamicalSystems", "CairoMakie", "OrdinaryDiffEq", "BenchmarkTools"]; mode = Pkg.PKGMODE_MANIFEST)

Status `~/work/DynamicalSystems.jl/DynamicalSystems.jl/docs/Manifest.toml`
  [6e4b80f9] BenchmarkTools v1.5.0
  [13f3f980] CairoMakie v0.12.17
  [61744808] DynamicalSystems v3.4.0
  [1dea7af3] OrdinaryDiffEq v6.90.1

Core components

The individual packages that compose DynamicalSystems interact flawlessly with each other because of the following two components:

1. The StateSpaceSet, which represents numerical data. They can be observed or measured from experiments, sampled trajectories of dynamical systems, or just unordered sets in a state space. A StateSpaceSet is a container of equally-sized points, representing multivariate timeseries or multivariate datasets. Timeseries, which are univariate sets, are represented by the AbstractVector{<:Real} Julia base type.
2. The DynamicalSystem, which is the abstract representation of a dynamical system with a known dynamic evolution rule. DynamicalSystem defines an extendable interface, but typically one uses existing implementations such as DeterministicIteratedMap or CoupledODEs.

Making dynamical systems

In the majority of cases, to make a dynamical system one needs three things:

1. The dynamic rule f: A Julia function that provides the instructions of how to evolve the dynamical system in time.
2. The state u: An array-like container that contains the variables of the dynamical system and also defines the starting state of the system.
3. The parameters p: An arbitrary container that parameterizes f.

For most concrete implementations of DynamicalSystem there are two ways of defining f, u. The distinction is done on whether f is defined as an in-place (iip) function or out-of-place (oop) function.

• oop : f must be in the form f(u, p, t) -> out which means that given a state u::SVector{<:Real} and some parameter container p it returns the output of f as an SVector{<:Real} (static vector).
• iip : f must be in the form f!(out, u, p, t) which means that given a state u::AbstractArray{<:Real} and some parameter container p, it writes in-place the output of f in out::AbstractArray{<:Real}. The function must return nothing as a final statement.

t stands for current time in both cases. iip is suggested for systems with high dimension and oop for small. The break-even point is between 10 to 100 dimensions but should be benchmarked on a case-by-case basis as it depends on the complexity of f.

Example: Henon map

Let's make the Henon map, defined as

\[\begin{aligned} x_{n+1} &= 1 - ax^2_n+y_n \\ y_{n+1} & = bx_n \end{aligned}\]

with parameters $a = 1.4, b = 0.3$.

First, we define the dynamic rule as a standard Julia function. Since the dynamical system is only two-dimensional, we should use the out-of-place form that returns an SVector with the next state:

using DynamicalSystems

function henon_rule(u, p, n) # here `n` is "time", but we don't use it.
    x, y = u # system state
    a, b = p # system parameters
    xn = 1.0 - a*x^2 + y
    yn = b*x
    return SVector(xn, yn)
end

henon_rule (generic function with 1 method)

Then, we define initial state and parameters

u0 = [0.2, 0.3]
p0 = [1.4, 0.3]

2-element Vector{Float64}:
 1.4
 0.3

Lastly, we give these three to the DeterministicIteratedMap:

henon = DeterministicIteratedMap(henon_rule, u0, p0)

2-dimensional DeterministicIteratedMap
 deterministic: true
 discrete time: true
 in-place:      false
 dynamic rule:  henon_rule
 parameters:    [1.4, 0.3]
 time:          0
 state:         [0.2, 0.3]

henon is a DynamicalSystem, one of the two core structures of the library. They can evolved interactively, and queried, using the interface defined by DynamicalSystem. The simplest thing you can do with a DynamicalSystem is to get its trajectory:

total_time = 10_000
X, t = trajectory(henon, total_time)
X

2-dimensional StateSpaceSet{Float64} with 10001 points
  0.2        0.3
  1.244      0.06
 -1.10655    0.3732
 -0.341035  -0.331965
  0.505208  -0.102311
  0.540361   0.151562
  0.742777   0.162108
  0.389703   0.222833
  1.01022    0.116911
 -0.311842   0.303065
  ⋮         
 -0.582534   0.328346
  0.853262  -0.17476
 -0.194038   0.255978
  1.20327   -0.0582113
 -1.08521    0.36098
 -0.287758  -0.325562
  0.558512  -0.0863275
  0.476963   0.167554
  0.849062   0.143089

X is a StateSpaceSet, the second of the core structures of the library. We'll see below how, and where, to use a StateSpaceset, but for now let's just do a scatter plot

using CairoMakie
scatter(X)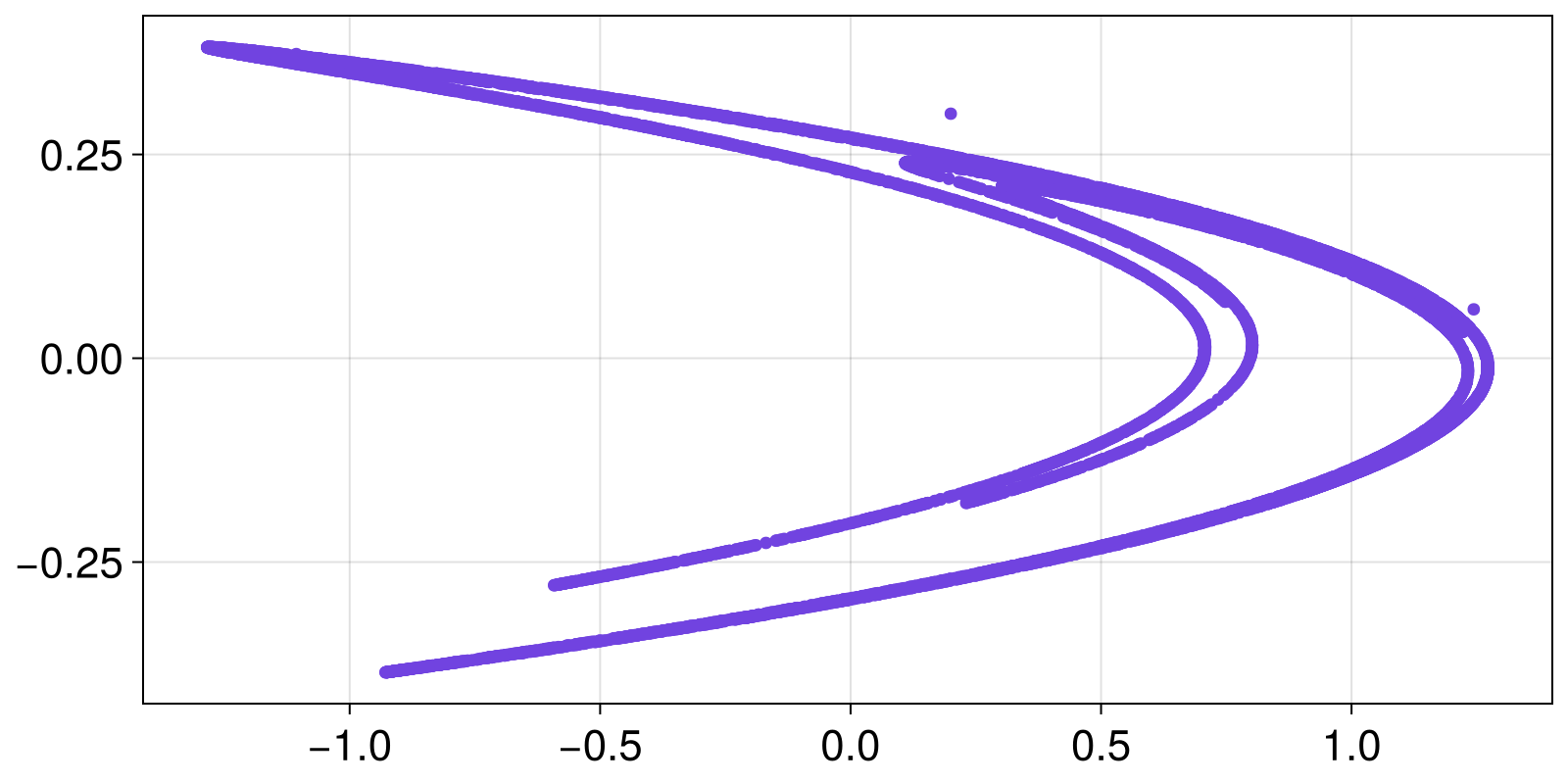

Example: Lorenz96

Let's also make another dynamical system, the Lorenz96 model:

\[\frac{dx_i}{dt} = (x_{i+1}-x_{i-2})x_{i-1} - x_i + F\]

for $i \in \{1, \ldots, N\}$ and $N+j=j$.

Here, instead of a discrete time map we have $N$ coupled ordinary differential equations. However, creating the dynamical system works out just like above, but using CoupledODEs instead of DeterministicIteratedMap.

First, we make the dynamic rule function. Since this dynamical system can be arbitrarily high-dimensional, we prefer to use the in-place form for f, overwriting in place the rate of change in a pre-allocated container. It is customary to append the name of functions that modify their arguments in-place with a bang (!).

function lorenz96_rule!(du, u, p, t)
    F = p[1]; N = length(u)
    # 3 edge cases
    du[1] = (u[2] - u[N - 1]) * u[N] - u[1] + F
    du[2] = (u[3] - u[N]) * u[1] - u[2] + F
    du[N] = (u[1] - u[N - 2]) * u[N - 1] - u[N] + F
    # then the general case
    for n in 3:(N - 1)
        du[n] = (u[n + 1] - u[n - 2]) * u[n - 1] - u[n] + F
    end
    return nothing # always `return nothing` for in-place form!
end

lorenz96_rule! (generic function with 1 method)

then, like before, we define an initial state and parameters, and initialize the system

N = 6
u0 = range(0.1, 1; length = N)
p0 = [8.0]
lorenz96 = CoupledODEs(lorenz96_rule!, u0, p0)

6-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      true
 dynamic rule:  lorenz96_rule!
 ODE solver:    Tsit5
 ODE kwargs:    (abstol = 1.0e-6, reltol = 1.0e-6)
 parameters:    [8.0]
 time:          0.0
 state:         [0.1, 0.28, 0.46, 0.64, 0.82, 1.0]

and, again like before, we may obtain a trajectory the same way

total_time = 12.5
sampling_time = 0.02
Y, t = trajectory(lorenz96, total_time; Ttr = 2.2, Δt = sampling_time)
Y

6-dimensional StateSpaceSet{Float64} with 626 points
  3.15368   -4.40493  0.0311581  0.486735  1.89895   4.15167
  2.71382   -4.39303  0.395019   0.66327   2.0652    4.32045
  2.25088   -4.33682  0.693967   0.879701  2.2412    4.46619
  1.7707    -4.24045  0.924523   1.12771   2.42882   4.58259
  1.27983   -4.1073   1.08656    1.39809   2.62943   4.66318
  0.785433  -3.94005  1.18319    1.6815    2.84384   4.70147
  0.295361  -3.74095  1.2205     1.96908   3.07224   4.69114
 -0.181932  -3.51222  1.20719    2.25296   3.3139    4.62628
 -0.637491  -3.25665  1.154      2.5267    3.56698   4.50178
 -1.06206   -2.9781   1.07303    2.7856    3.82827   4.31366
  ⋮                                                  ⋮
  3.17245    2.3759   3.01796    7.27415   7.26007  -0.116002
  3.29671    2.71146  3.32758    7.5693    6.75971  -0.537853
  3.44096    3.09855  3.66908    7.82351   6.13876  -0.922775
  3.58387    3.53999  4.04452    8.01418   5.39898  -1.25074
  3.70359    4.03513  4.45448    8.1137    4.55005  -1.5042
  3.78135    4.57879  4.89677    8.09013   3.61125  -1.66943
  3.80523    5.16112  5.36441    7.90891   2.61262  -1.73822
  3.77305    5.7684   5.84318    7.53627   1.59529  -1.71018
  3.6934     6.38507  6.30923    6.94454   0.61023  -1.59518

We can't scatterplot something 6-dimensional but we can visualize all timeseries

fig = Figure()
ax = Axis(fig[1, 1]; xlabel = "time", ylabel = "variable")
for var in columns(Y)
    lines!(ax, t, var)
end
fig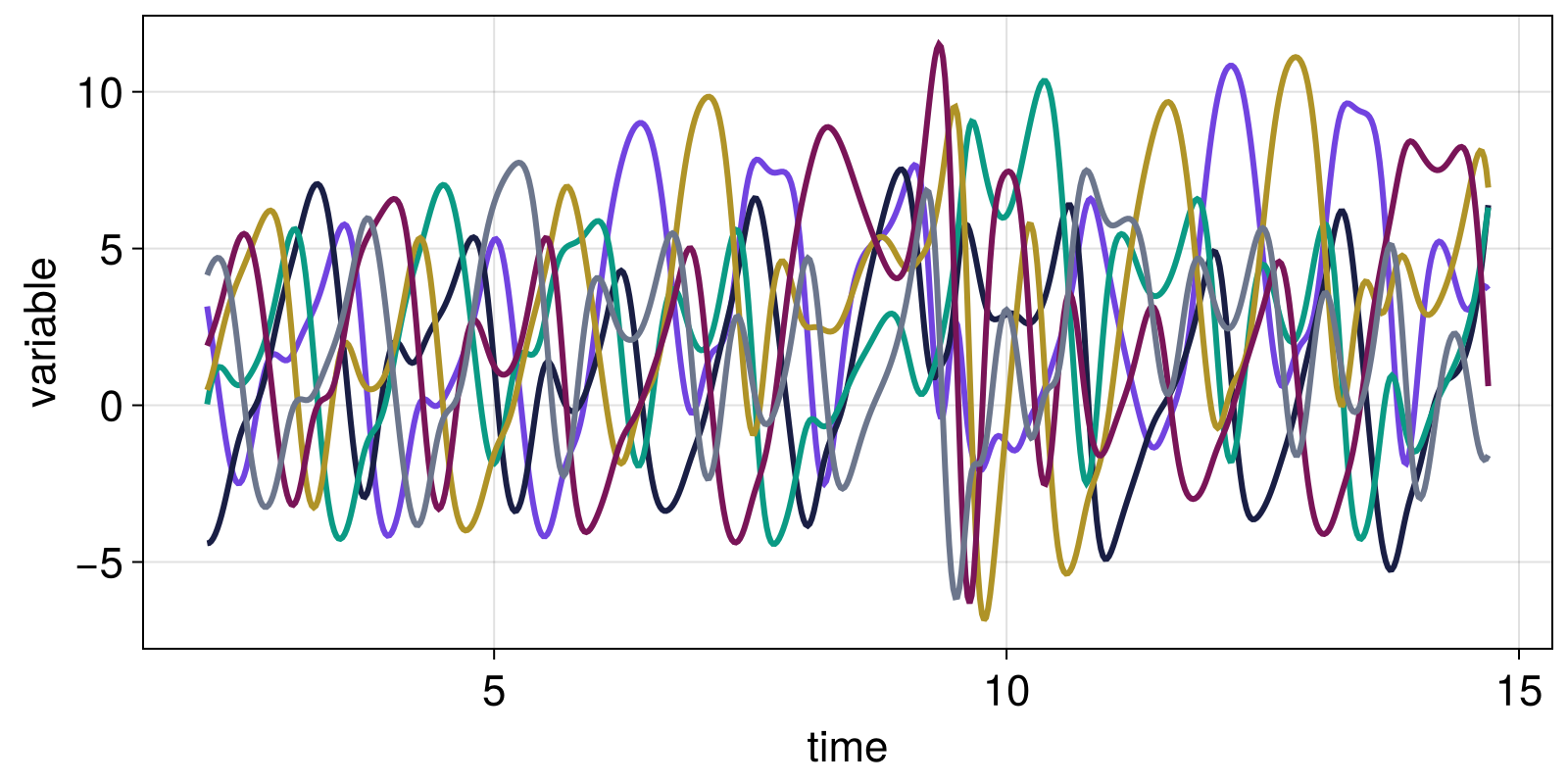

ODE solving and choosing solver

Continuous time dynamical systems are evolved through DifferentialEquations.jl. In this sense, the above trajectory function is a simplified version of DifferentialEquations.solve. If you only care about evolving a dynamical system forwards in time, you are probably better off using DifferentialEquations.jl directly. DynamicalSystems.jl can be used to do many other things that either occur during the time evolution or after it, see the section below on using dynamical systems.

When initializing a CoupledODEs you can tune the solver properties to your heart's content using any of the ODE solvers and any of the common solver options. For example:

using OrdinaryDiffEq: Vern9 # accessing the ODE solvers
diffeq = (alg = Vern9(), abstol = 1e-9, reltol = 1e-9)
lorenz96_vern = ContinuousDynamicalSystem(lorenz96_rule!, u0, p0; diffeq)

6-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      true
 dynamic rule:  lorenz96_rule!
 ODE solver:    Vern9
 ODE kwargs:    (abstol = 1.0e-9, reltol = 1.0e-9)
 parameters:    [8.0]
 time:          0.0
 state:         [0.1, 0.28, 0.46, 0.64, 0.82, 1.0]

Y, t = trajectory(lorenz96_vern, total_time; Ttr = 2.2, Δt = sampling_time)
Y[end]

6-element SVector{6, Float64} with indices SOneTo(6):
  3.839024812256864
  6.155709531152434
  6.080625689022988
  7.278588308991119
  1.2582152212922841
 -1.52970629168123

The choice of the solver algorithm can have huge impact on the performance and stability of the ODE integration! We will showcase this with two simple examples

Higher accuracy, higher order

The solver Tsit5 (the default solver) is most performant when medium-low error tolerances are requested. When we require very small error tolerances, choosing a different solver can be more accurate. This can be especially impactful for chaotic dynamical systems. Let's first expliclty ask for a given accuracy when solving the ODE by passing the keywords abstol, reltol (for absolute and relative tolerance respectively), and compare performance to a naive solver one would use:

using BenchmarkTools: @btime
using OrdinaryDiffEq: BS3 # 3rd order solver

for alg in (BS3(), Vern9())
    diffeq = (; alg, abstol = 1e-12, reltol = 1e-12)
    lorenz96 = CoupledODEs(lorenz96_rule!, u0, p0; diffeq)
    @btime step!($lorenz96, 100.0) # evolve for 100 time units
end

┌ Warning: Assignment to `diffeq` in soft scope is ambiguous because a global variable by the same name exists: `diffeq` will be treated as a new local. Disambiguate by using `local diffeq` to suppress this warning or `global diffeq` to assign to the existing global variable.
└ @ tutorial.md:229
┌ Warning: Assignment to `lorenz96` in soft scope is ambiguous because a global variable by the same name exists: `lorenz96` will be treated as a new local. Disambiguate by using `local lorenz96` to suppress this warning or `global lorenz96` to assign to the existing global variable.
└ @ tutorial.md:230
  622.698 ms (0 allocations: 0 bytes)
  2.544 ms (0 allocations: 0 bytes)

The performance difference is dramatic!

Stiff problems

A "stiff" ODE problem is one that can be numerically unstable unless the step size (or equivalently, the step error tolerances) are extremely small. There are several situations where a problem may be come "stiff":

• The derivative values can get very large for some state values.
• There is a large timescale separation between the dynamics of the variables
• There is a large speed separation between different state space regions

One must be aware whether this is possible for their system and choose a solver that is better suited to tackle stiff problems. If not, a solution may diverge and the ODE integrator will throw an error or a warning.

Many of the problems in DifferentialEquations.jl are suitable for dealing with stiff problems. We can create a stiff problem by using the well known Van der Pol oscillator with a timescale separation:

\[\begin{aligned} \dot{x} & = y \\ \dot{y} / \mu &= (1-x^2)y - x \end{aligned}\]

with $\mu$ being the timescale of the $y$ variable in units of the timescale of the $x$ variable. For very large values of $\mu$ this problem becomes stiff.

Let's compare

using OrdinaryDiffEq: Tsit5, Rodas5P

function vanderpol_rule(u, μ, t)
    x, y = u
    dx = y
    dy = μ*((1-x^2)*y - x)
    return SVector(dx, dy)
end

μ = 1e6

for alg in (Tsit5(), Rodas5P()) # default vs specialized solver
    diffeq = (; alg, abstol = 1e-12, reltol = 1e-12, maxiters = typemax(Int))
    vdp = CoupledODEs(vanderpol_rule, SVector(1.0, 1.0), μ; diffeq)
    @btime step!($vdp, 100.0)
end

┌ Warning: Assignment to `diffeq` in soft scope is ambiguous because a global variable by the same name exists: `diffeq` will be treated as a new local. Disambiguate by using `local diffeq` to suppress this warning or `global diffeq` to assign to the existing global variable.
└ @ tutorial.md:273
  9.313 s (0 allocations: 0 bytes)
  646.298 ms (5865212 allocations: 939.71 MiB)

We see that the stiff solver Rodas5P is much faster than the default Tsit5 when there is a large timescale separation. This happened because Rodas5P required much less steps to integrated the same total amount of time. In fact, there are cases where regular solvers will fail to integrate the ODE if the problem is very stiff, e.g. in the ROBER example.

So using an appropriate solver really does matter! For more information on choosing solvers consult the DifferentialEquations.jl documentation.

Interacting with dynamical systems

The DynamicalSystem type defines an extensive interface for what it means to be a "dynamical system". This interface can be used to (1) define fundamentally new types of dynamical systems, (2) to develop algorithms that utilize dynamical systems with a known evolution rule. It can also be used to simply query and alter properties of a given dynamical system. For example, we have

lorenz96

6-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      true
 dynamic rule:  lorenz96_rule!
 ODE solver:    Tsit5
 ODE kwargs:    (abstol = 1.0e-6, reltol = 1.0e-6)
 parameters:    [8.0]
 time:          14.701155497930898
 state:         [3.6876852333269934, 6.4206642171203905, 6.3350954379544815, 6.903266987356904, 0.5554923505362, -1.5862763310507715]

which we can evolve forwards in time using step!

step!(lorenz96, 100.0) # progress for `100.0` units of time

6-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      true
 dynamic rule:  lorenz96_rule!
 ODE solver:    Tsit5
 ODE kwargs:    (abstol = 1.0e-6, reltol = 1.0e-6)
 parameters:    [8.0]
 time:          114.71418312181382
 state:         [-5.045856737464552, 3.34756648658165, 1.7971515648478047, 2.1103433258068325, 7.912486267903331, 7.460799029710482]

and we can then query what is the current state that the dynamical system was brought into

current_state(lorenz96)

6-element Vector{Float64}:
 -5.045856737464552
  3.34756648658165
  1.7971515648478047
  2.1103433258068325
  7.912486267903331
  7.460799029710482

we can also restart the system at a different state using set_state!

set_state!(lorenz96, rand(6))

6-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      true
 dynamic rule:  lorenz96_rule!
 ODE solver:    Tsit5
 ODE kwargs:    (abstol = 1.0e-6, reltol = 1.0e-6)
 parameters:    [8.0]
 time:          114.71418312181382
 state:         [0.04914497156592679, 0.9520036817466555, 0.5245935273535138, 0.6726700064151965, 0.3942380358552239, 0.1311983820781195]

or we can alter system parameters given the index of the parameter and the value to set it to

set_parameter!(lorenz96, 1, 9.6) # change first parameter of the parameter container
current_parameters(lorenz96)

1-element Vector{Float64}:
 9.6

For more functions that query or alter a dynamical system see its docstring: DynamicalSystem.

Using dynamical systems

Now, as an end-user, you are most likely to be giving a DynamicalSystem instance to a library function. For example, you may want to compute the Lyapunov spectrum of the Lorenz96 system from above, which is a functionality offered by ChaosTools. This is as easy as calling the lyapunovspectrum function with lorenz96

steps = 10_000
lyapunovspectrum(lorenz96, steps)

6-element Vector{Float64}:
  1.213769239293399
  0.0005346998238078642
 -0.12430244395216608
 -0.8296328685052938
 -1.5959418017436058
 -4.664423704523864

As expected, there is at least one positive Lyapunov exponent, because the system is chaotic, and at least one zero Lyapunov exponent, because the system is continuous time.

A fantastic feature of DynamicalSystems.jl is that all library functions work for any applicable dynamical system. The exact same lyapunovspectrum function would also work for the Henon map.

lyapunovspectrum(henon, steps)

2-element Vector{Float64}:
  0.4167659070649148
 -1.6207387113908505

Something else that uses a dynamical system is estimating the basins of attraction of a multistable dynamical system. The Henon map is "multistable" in the sense that some initial conditions diverge to infinity, and some others converge to a chaotic attractor. Computing these basins of attraction is simple with Attractors, and would work as follows:

# define a state space grid to compute the basins on:
xg = yg = range(-2, 2; length = 201)
# find attractors using recurrences in state space:
mapper = AttractorsViaRecurrences(henon, (xg, yg); sparse = false)
# compute the full basins of attraction:
basins, attractors = basins_of_attraction(mapper; show_progress = false)

([-1 -1 … -1 -1; -1 -1 … -1 -1; … ; -1 -1 … -1 -1; -1 -1 … -1 -1], Dict{Int64, StateSpaceSet{2, Float64, SVector{2, Float64}}}(1 => 2-dimensional StateSpaceSet{Float64} with 416 points))

Let's visualize the result

heatmap_basins_attractors((xg, yg), basins, attractors)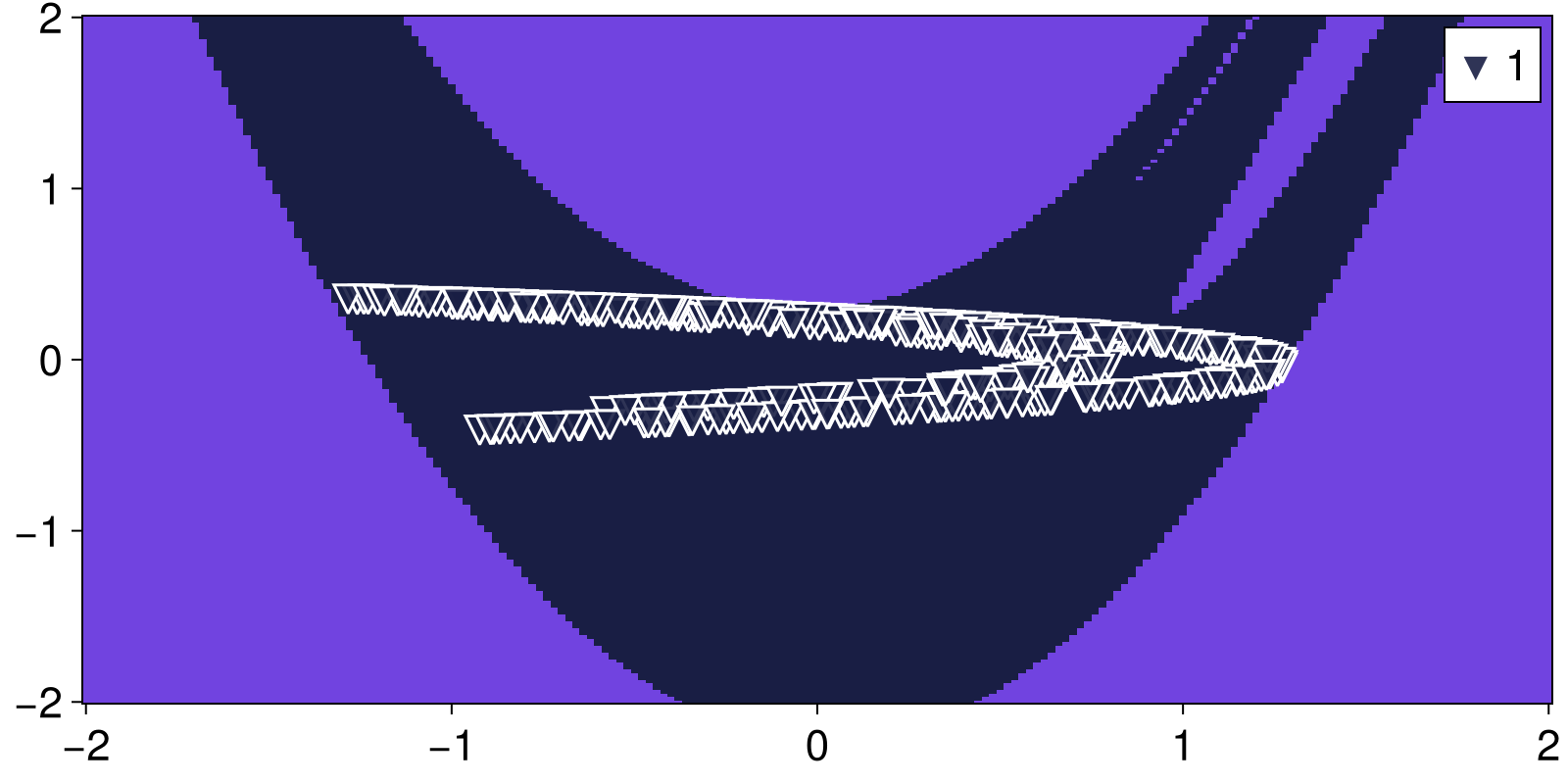

Stochastic systems

DynamicalSystems.jl has some support for stochastic systems in the form of Stochastic Differential Equations (SDEs). Just like CoupledODEs, one can make CoupledSDEs! For example here is a stochastic version of a FitzHugh-Nagumo model

using StochasticDiffEq # load extention for `CoupledSDEs`

function fitzhugh_nagumo(u, p, t)
    x, y = u
    ϵ, β, α, γ, κ, I = p
    dx = (-α * x^3 + γ * x - κ * y + I) / ϵ
    dy = -β * y + x
    return SVector(dx, dy)
end
p = [1.,3.,1.,1.,1.,0.]
sde = CoupledSDEs(fitzhugh_nagumo, zeros(2), p; noise_strength = 0.05)

2-dimensional CoupledSDEs
 deterministic: false
 discrete time: false
 in-place:      false
 dynamic rule:  fitzhugh_nagumo
 SDE solver:    SOSRA
 SDE kwargs:    (abstol = 0.01, reltol = 0.01, dt = 0.1)
 Noise type:    (additive = true, autonomous = true, linear = true, invertible = true)
 parameters:    [1.0, 3.0, 1.0, 1.0, 1.0, 0.0]
 time:          0.0
 state:         [0.0, 0.0]

In this particular example the SDE noise is white noise (Wiener process) with strength (σ) of 0.05. See the documentation of CoupledSDEs for alternatives.

In any case, in DynamicalSystems.jl all dynamical systems are part of the same interace, stochastic or not. As long as the algorithm is not influenced by stochasticity, we can apply it to CoupledSDEs just as well. For example, we can study multistability in a stochastic system. In contrast to the previous example of the Henon map, we have to use an alternative algorithm, because AttractorsViaRecurrences only works for deterministic systems. So instead we'll use AttractorsViaFeaturizing:

featurizer(X, t) = X[end]

mapper = AttractorsViaFeaturizing(sde, featurizer; Ttr = 200, T = 10)

xg = yg = range(-1, 1; length = 101)

sampler, _ = statespace_sampler((xg, yg))

fs = basins_fractions(mapper, sampler; show_progress = false)

Dict{Int64, Float64} with 2 entries:
  2 => 0.483
  1 => 0.517

and we can see the stored "attractors"

attractors = extract_attractors(mapper)
fig, ax = scatter(attractors[1])
scatter!(attractors[2])
fig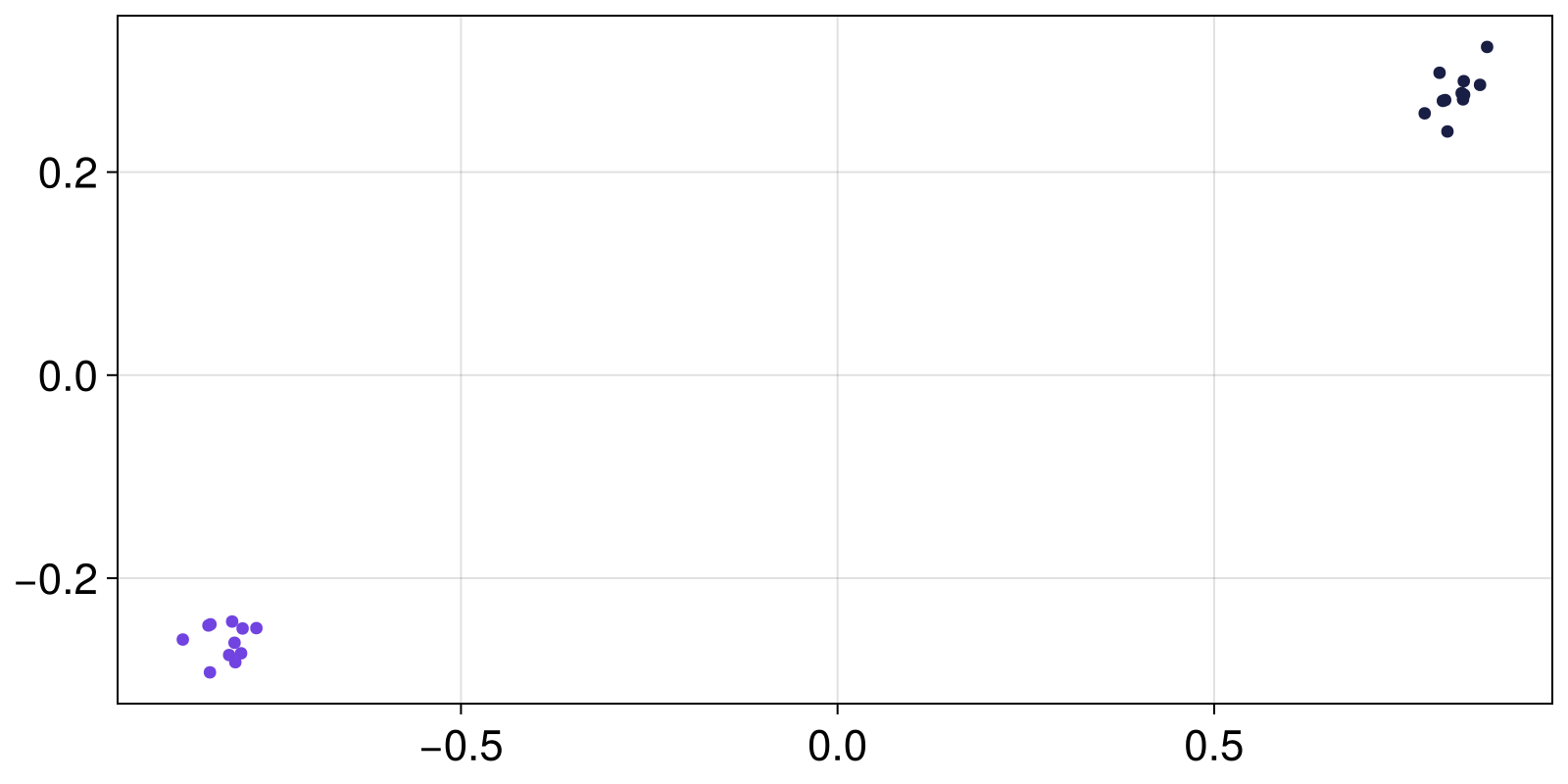

The mathematical concept of attractors doesn't translate trivially to stochastic systems but thankfully this system has two fixed point attractors that are only mildly perturbed by the noise.

Parallelization

Since DynamicalSystems are mutable, one needs to copy them before parallelizing, to avoid having to deal with complicated race conditions etc. The simplest way is with deepcopy. Here is an example block that shows how to parallelize calling some expensive function (e.g., calculating the Lyapunov exponent) over a parameter range (or alternatively, over different initial conditions) using Threads:

ds = DynamicalSystem(f, u, p) # some concrete implementation
parameters = 0:0.01:1
outputs = zeros(length(parameters))

# Since `DynamicalSystem`s are mutable, we need to copy to parallelize
systems = [deepcopy(ds) for _ in 1:Threads.nthreads()-1]
pushfirst!(systems, ds) # we can save 1 copy

Threads.@threads for (i, p) in enumerate(parameters)
    system = systems[Threads.threadid()]
    set_parameter!(system, index, parameters[i])
    outputs[i] = expensive_function(system, args...)
end

Interactive GUIs

A particularly useful feature are interactive GUI apps one can launch to examine a DynamicalSystem. The simplest is interactive_trajectory_timeseries. To actually make it interactive one needs to enable GLMakie.jl as a backend:

import GLMakie
GLMakie.activate!()

and then launch the app:

u0s = [10rand(5) for _ in 1:3]
parameter_sliders = Dict(1 => 0:0.01:32)

fig, dsobs = interactive_trajectory_timeseries(
    lorenz96, [1, 2, 3, 4, 5], u0s;
    Δt = 0.02, parameter_sliders
)
fig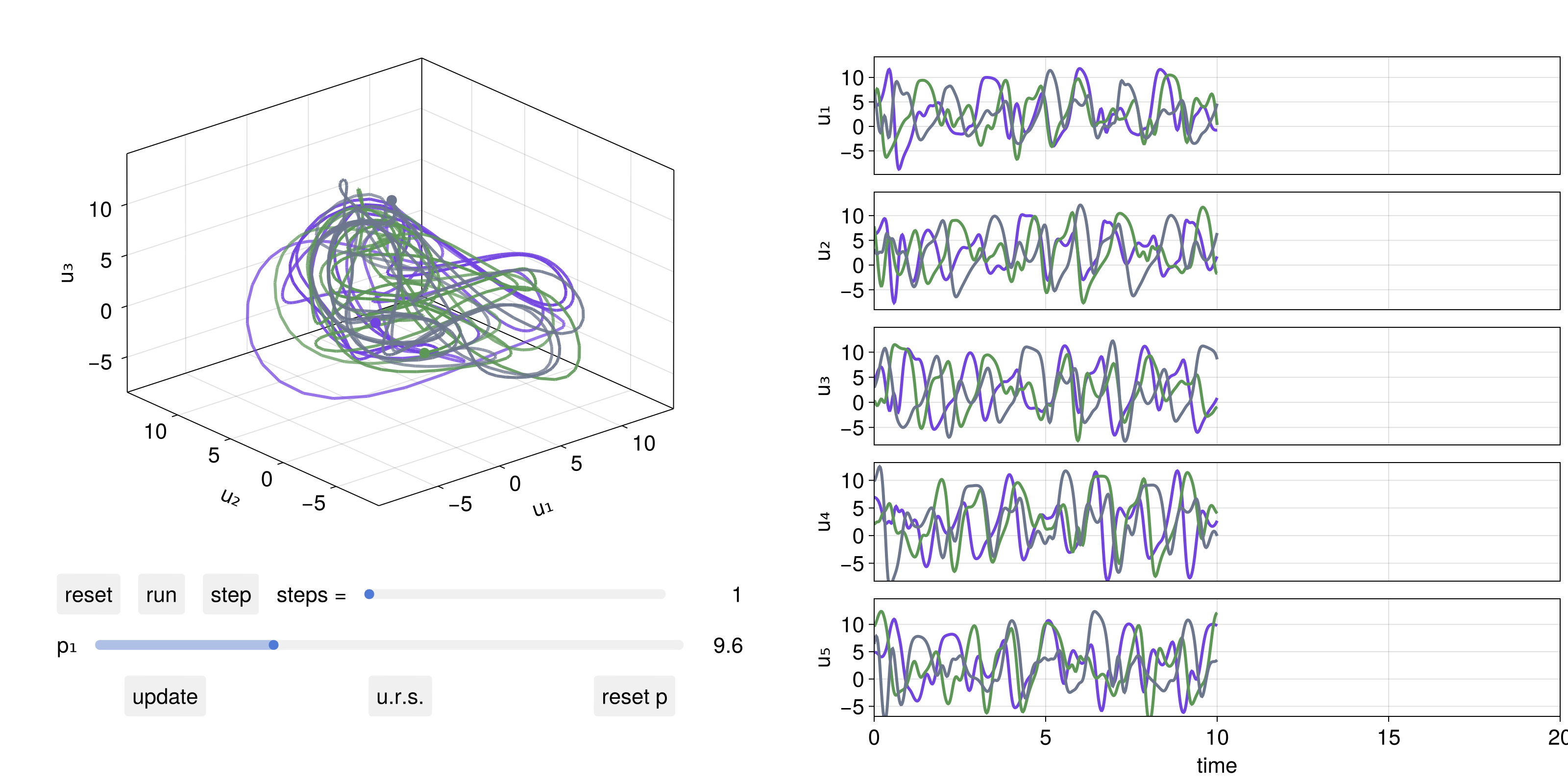

Developing new algorithms

You could also be using a DynamicalSystem instance directly to build your own algorithm if it isn't already implemented (and then later contribute it so it is implemented ;) ). A dynamical system can be evolved forwards in time using step!:

henon

2-dimensional DeterministicIteratedMap
 deterministic: true
 discrete time: true
 in-place:      false
 dynamic rule:  henon_rule
 parameters:    [1.4, 0.3]
 time:          5
 state:         [-1.5266434026801804e8, -3132.7519146699206]

Notice how the time is not 0, because henon has already been stepped when we called the function basins_of_attraction with it. We can step it more:

step!(henon)

2-dimensional DeterministicIteratedMap
 deterministic: true
 discrete time: true
 in-place:      false
 dynamic rule:  henon_rule
 parameters:    [1.4, 0.3]
 time:          6
 state:         [-3.262896110526e16, -4.579930208040541e7]

step!(henon, 2)

2-dimensional DeterministicIteratedMap
 deterministic: true
 discrete time: true
 in-place:      false
 dynamic rule:  henon_rule
 parameters:    [1.4, 0.3]
 time:          8
 state:         [-3.110262842032839e66, -4.4715262317959936e32]

For more information on how to directly use DynamicalSystem instances, see the documentation of DynamicalSystemsBase.

State space sets

Let's recall that the output of the trajectory function is a StateSpaceSet:

X

2-dimensional StateSpaceSet{Float64} with 10001 points
  0.2        0.3
  1.244      0.06
 -1.10655    0.3732
 -0.341035  -0.331965
  0.505208  -0.102311
  0.540361   0.151562
  0.742777   0.162108
  0.389703   0.222833
  1.01022    0.116911
 -0.311842   0.303065
  ⋮         
 -0.582534   0.328346
  0.853262  -0.17476
 -0.194038   0.255978
  1.20327   -0.0582113
 -1.08521    0.36098
 -0.287758  -0.325562
  0.558512  -0.0863275
  0.476963   0.167554
  0.849062   0.143089

This is the main data structure used in DynamicalSystems.jl to handle numerical data. It is printed like a matrix where each column is the timeseries of each dynamic variable. In reality, it is a vector equally-sized vectors representing state space points. (For advanced users: StateSpaceSet directly subtypes AbstractVector{<:AbstractVector})

When indexed with 1 index, it behaves like a vector of vectors

X[1]

2-element SVector{2, Float64} with indices SOneTo(2):
 0.2
 0.3

X[2:5]

2-dimensional StateSpaceSet{Float64} with 4 points
  1.244      0.06
 -1.10655    0.3732
 -0.341035  -0.331965
  0.505208  -0.102311

When indexed with two indices, it behaves like a matrix

X[7:13, 2] # 2nd column

7-element Vector{Float64}:
  0.1621081681101694
  0.22283309461548204
  0.11691103950545975
  0.30306503631282444
 -0.09355263057973214
  0.35007640234803744
 -0.29998206408499634

When iterated, it iterates over the contained points

for (i, point) in enumerate(X)
    @show point
    i > 5 && break
end

point = [0.2, 0.3]
point = [1.244, 0.06]
point = [-1.1065503999999997, 0.3732]
point = [-0.34103530283622296, -0.3319651199999999]
point = [0.5052077711071681, -0.10231059085086688]
point = [0.5403605603672313, 0.1515623313321504]

map(point -> point[1] + 1/(point[2]+0.1), X)

10001-element Vector{Float64}:
    2.7
    7.494
    1.006720944040575
   -4.652028265916192
 -432.28452634595817
    4.515518505137784
    4.557995741581754
    3.4872793228808314
    5.620401692451571
    2.1691470931310732
    ⋮
    1.752024323892008
  -12.522817477226136
    2.6151207744662046
   25.133206775921803
    1.0840850677362275
   -4.721137673509619
   73.69787164232238
    4.214533120554577
    4.9627832739756785

The columns of the set are obtained with the convenience columns function

x, y = columns(X)
summary.((x, y))

("10001-element Vector{Float64}", "10001-element Vector{Float64}")

Because StateSpaceSet really is a vector of vectors, it can be given to any Julia function that accepts such an input. For example, the Makie plotting ecosystem knows how to plot vectors of vectors. That's why this works:

scatter(X)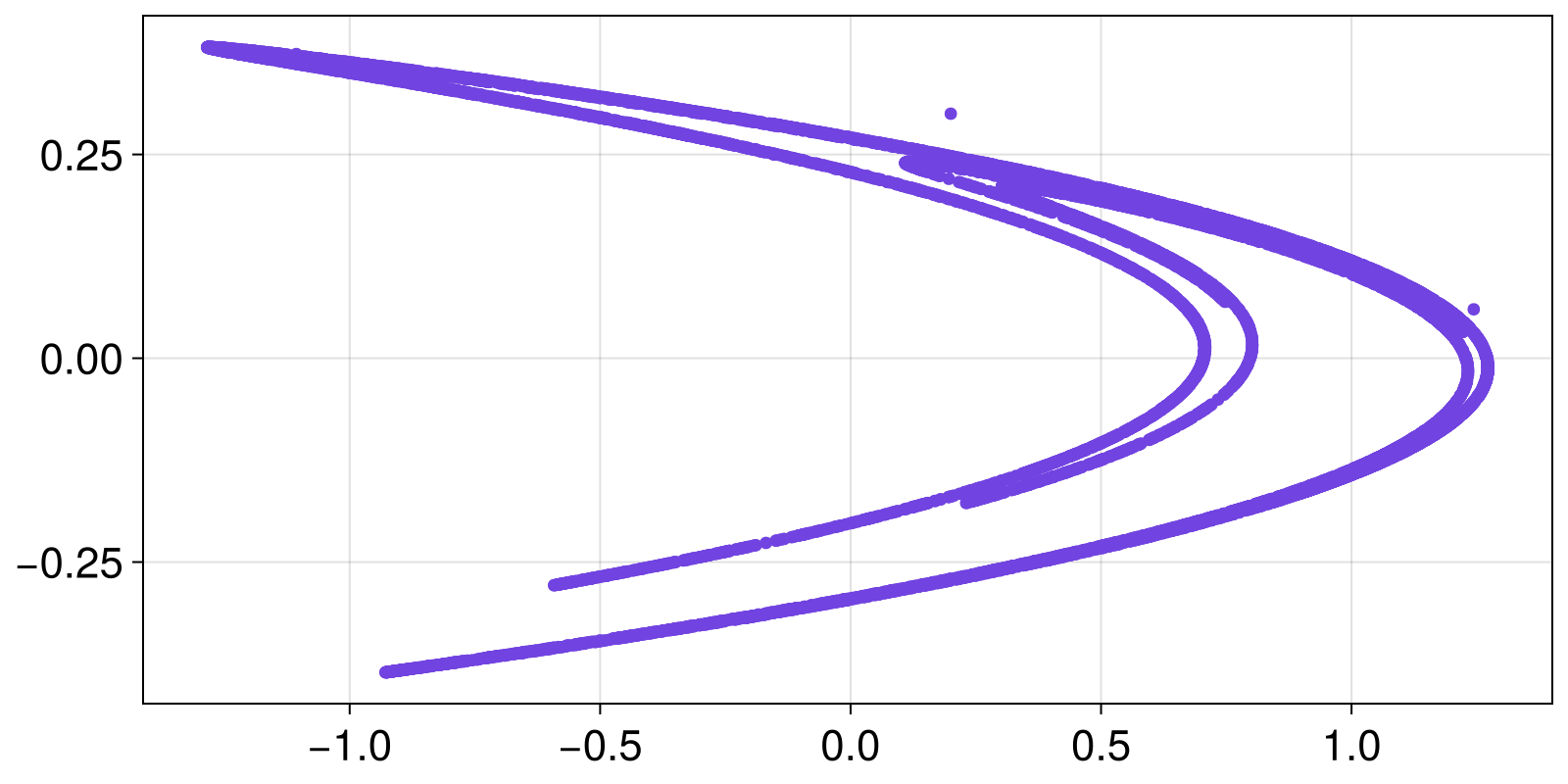

even though Makie has no knowledge of the specifics of StateSpaceSet.

Using state space sets

Several packages of the library deal with StateSpaceSets.

You could use ComplexityMeasures to obtain the entropy, or other complexity measures, of a given set. Below, we obtain the entropy of the natural density of the chaotic attractor by partitioning into a histogram of approximately 50 bins per dimension:

prob_est = ValueHistogram(50)
entropy(prob_est, X)

7.825799208736613

Or, obtain the permutation and sample entropies of the two columns of X:

pex = entropy_permutation(x; m = 4)
sey = entropy_sample(y; m = 2)
pex, sey

(3.15987571159201, 0.02579132263914716)

Alternatively, you could use FractalDimensions to get the fractal dimensions of the chaotic attractor of the henon map using the Grassberger-Procaccia algorithm:

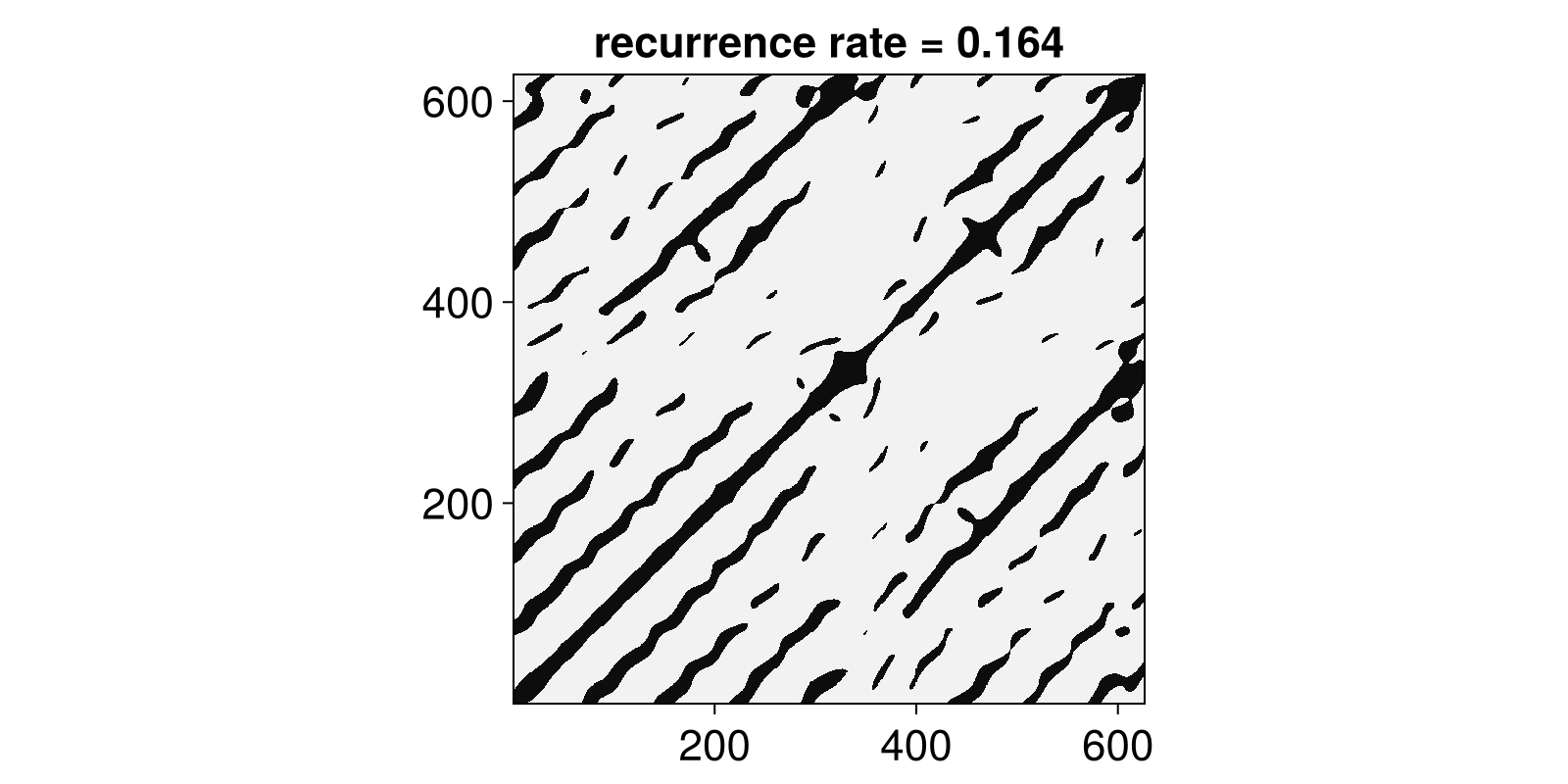
grassberger_proccacia_dim(X; show_progress = false)

1.2232922815092426

Or, you could obtain a recurrence matrix of a state space set with RecurrenceAnalysis

R = RecurrenceMatrix(Y, 8.0)
Rg = grayscale(R)
rr = recurrencerate(R)
heatmap(Rg; colormap = :grays,
    axis = (title = "recurrence rate = $(round(rr; digits = 3))", aspect = 1)
)

More nonlinear timeseries analysis

A trajectory of a known dynamical system is one way to obtain a StateSpaceSet. However, another common way is via a delay coordinates embedding of a measured/observed timeseries. For example, we could use optimal_separated_de from DelayEmbeddings to create an optimized delay coordinates embedding of a timeseries

w = Y[:, 1] # first variable of Lorenz96
𝒟, τ, e = optimal_separated_de(w)
𝒟

5-dimensional StateSpaceSet{Float64} with 558 points
  3.15369   -2.40036    1.60497   2.90499  5.72572
  2.71384   -2.24811    1.55832   3.04987  5.6022
  2.2509    -2.02902    1.50499   3.20633  5.38629
  1.77073   -1.75077    1.45921   3.37699  5.07029
  1.27986   -1.42354    1.43338   3.56316  4.65003
  0.785468  -1.05974    1.43672   3.76473  4.12617
  0.295399  -0.673567   1.47423   3.98019  3.50532
 -0.181891  -0.280351   1.54635   4.20677  2.80048
 -0.637447   0.104361   1.64932   4.44054  2.03084
 -1.06201    0.465767   1.77622   4.67654  1.22067
  ⋮                                        
  7.42111    9.27879   -1.23936   5.15945  3.25618
  7.94615    9.22663   -1.64222   5.24344  3.34749
  8.40503    9.13776   -1.81947   5.26339  3.46932
  8.78703    8.99491   -1.77254   5.22631  3.60343
  9.08701    8.77963   -1.51823   5.13887  3.72926
  9.30562    8.47357   -1.08603   5.00759  3.82705
  9.4488     8.06029   -0.514333  4.83928  3.88137
  9.52679    7.52731    0.153637  4.6414   3.88458
  9.55278    6.86845    0.873855  4.42248  3.83902

and compare

fig = Figure()
axs = [Axis3(fig[1, i]) for i in 1:2]
for (S, ax) in zip((Y, 𝒟), axs)
    lines!(ax, S[:, 1], S[:, 2], S[:, 3])
end
fig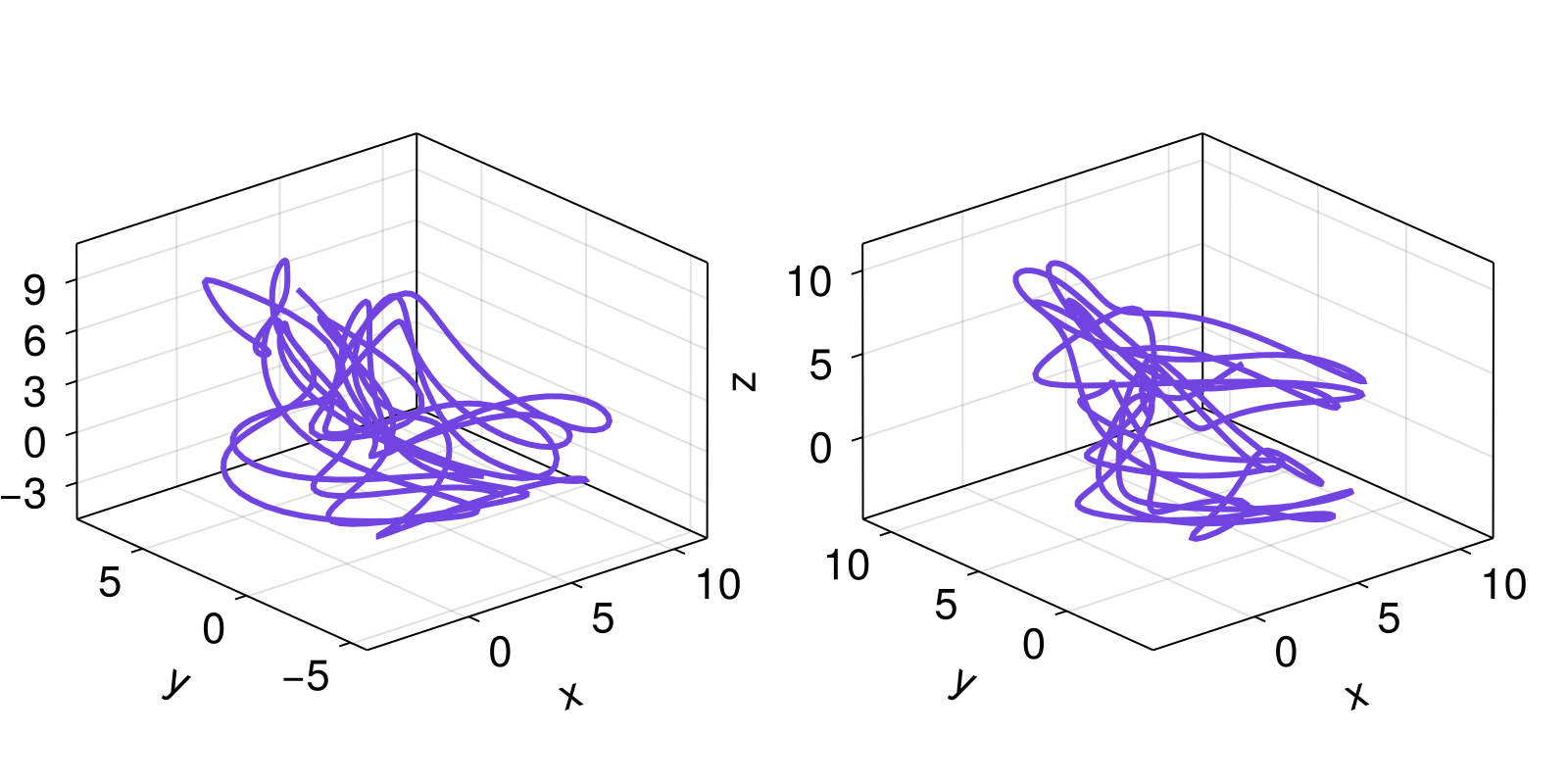

Since 𝒟 is just another state space set, we could be using any of the above analysis pipelines on it just as easily.

The last package to mention here is TimeseriesSurrogates, which ties with all other observed/measured data analysis by providing a framework for confidence/hypothesis testing. For example, if we had a measured timeseries but we were not sure whether it represents a deterministic system with structure in the state space, or mostly noise, we could do a surrogate test. For this, we use surrogenerator and RandomFourier from TimeseriesSurrogates, and the generalized_dim from FractalDimensions (because it performs better in noisy sets)

x # Henon map timeseries
# contaminate with noise
using Random: Xoshiro
rng = Xoshiro(1234)
x .+= randn(rng, length(x))/100
# compute noise-contaminated fractal dim.
Δ_orig = generalized_dim(embed(x, 2, 1); show_progress = false)

1.379868496235257

And we do the surrogate test

surrogate_method = RandomFourier()
sgen = surrogenerator(x, surrogate_method, rng)
Δ_surr = map(1:1000) do i
    s = sgen()
    generalized_dim(embed(s, 2, 1); show_progress = false)
end

1000-element Vector{Float64}:
 1.846942159464625
 1.8423032066769318
 1.829388076282451
 1.7971370517625704
 1.834567260935601
 1.8228426491504883
 1.8262488555662943
 1.8409915222341218
 1.8446289256464834
 1.821998418576316
 ⋮
 1.7896081624484643
 1.8207525706563554
 1.8314367557987012
 1.8026224878123838
 1.8550946797005674
 1.827878756277354
 1.8147474211321486
 1.8233116023793778
 1.814970850053253

and visualize the test result

fig, ax = hist(Δ_surr)
vlines!(ax, Δ_orig)
fig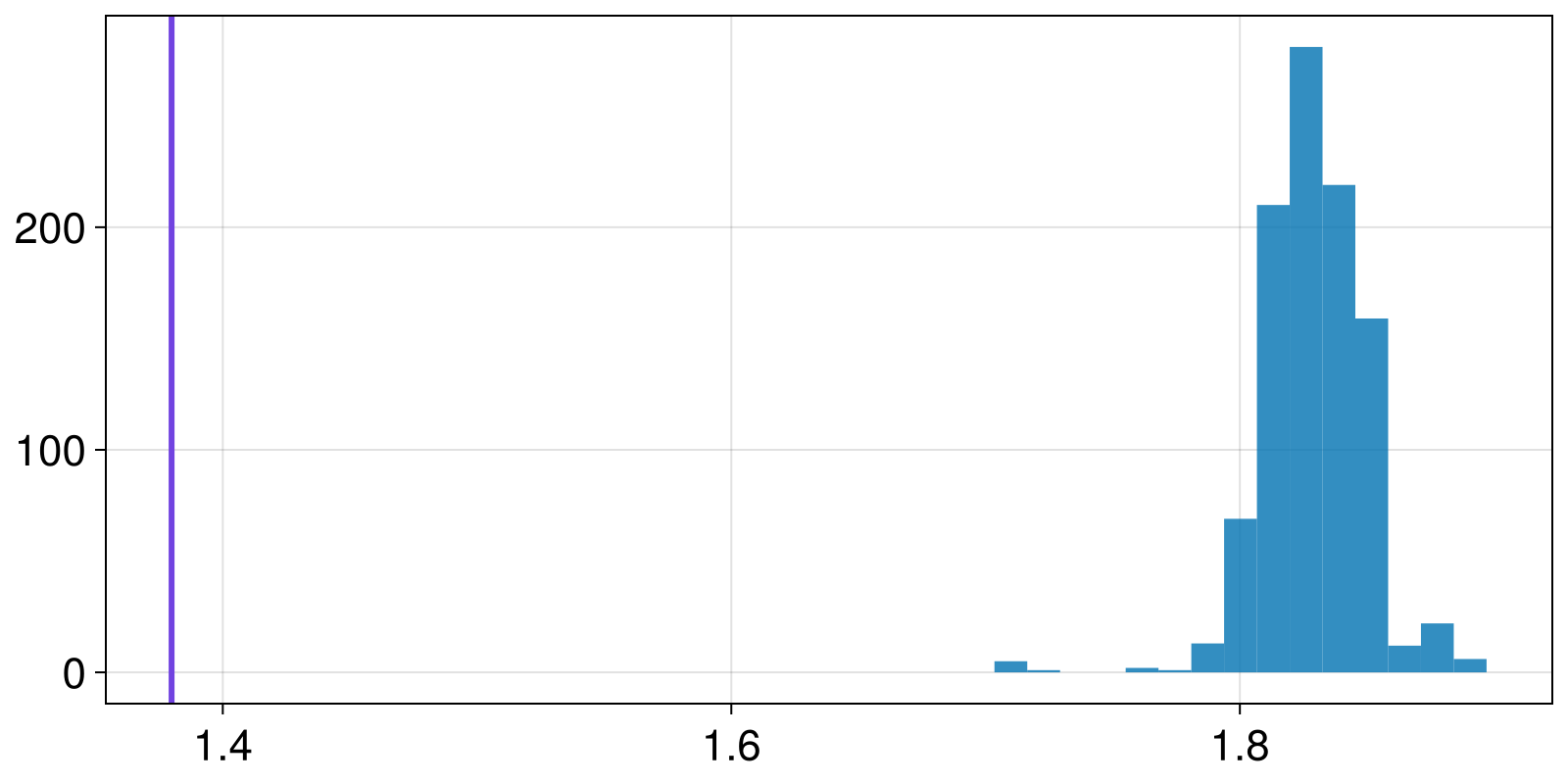

since the real value is outside the distribution we have confidence the data are not pure noise.

Integration with ModelingToolkit.jl

DynamicalSystems.jl understands when a model has been generated via ModelingToolkit.jl. The symbolic variables used in ModelingToolkit.jl can be used to access the state or parameters of the dynamical system.

To access this functionality, the DynamicalSystem must be created from a DEProblem of the SciML ecosystem, and the DEProblem itself must be created from a ModelingToolkit.jl model.

Let's create a the Roessler system as an MTK model:

using ModelingToolkit

@variables t # use unitless time
D = Differential(t)
@mtkmodel Roessler begin
    @parameters begin
        a = 0.2
        b = 0.2
        c = 5.7
    end
    @variables begin
        x(t) = 1.0
        y(t) = 0.0
        z(t) = 0.0
        nlt(t) # nonlinear term
    end
    @equations begin
        D(x) ~ -y -z
        D(y) ~ x + a*y
        D(z) ~ b + nlt
        nlt ~ z*(x - c)
    end
end

@mtkbuild model = Roessler()

\[ \begin{align} \frac{\mathrm{d} x\left( t \right)}{\mathrm{d}t} &= - y\left( t \right) - z\left( t \right) \\ \frac{\mathrm{d} y\left( t \right)}{\mathrm{d}t} &= x\left( t \right) + a y\left( t \right) \\ \frac{\mathrm{d} z\left( t \right)}{\mathrm{d}t} &= b + \mathtt{nlt}\left( t \right) \end{align} \]

this model can then be made into an ODEProblem:

prob = ODEProblem(model)

ODEProblem with uType Vector{Float64} and tType Nothing. In-place: true
timespan: (nothing, nothing)
u0: 3-element Vector{Float64}:
 1.0
 0.0
 0.0

(notice that because we specified initial values for all parameters and variables during the model creation we do need to provide additional initial values)

Now, this problem can be made into a CoupledODEs:

roessler = CoupledODEs(prob)

3-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      true
 dynamic rule:  f
 ODE solver:    Tsit5
 ODE kwargs:    (abstol = 1.0e-6, reltol = 1.0e-6)
 parameters:    ModelingToolkit.MTKParameters{Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}([0.2, 0.2, 5.7], (), (), (), ())
 time:          0.0
 state:         [1.0, 0.0, 0.0]

This dynamical system instance can be used in the rest of the library like anything else. Additionally, you can "observe" referenced symbolic variables:

observe_state(roessler, model.x)

1.0

or, more commonly, you can observe a Symbol that has the name of the symbolic variable:

observe_state(roessler, :nlt)

-0.0

These observables can also be used in the GUI visualization interactive_trajectory_timeseries.

You can also symbolically alter parameters

current_parameter(roessler, :c)

5.7

set_parameter!(roessler, :c, 5.0)

current_parameter(roessler, :c)

5.0

This symbolic indexing can be given anywhere in the ecosystem where you would be altering the parameters, such as the function global_continuation from Attractors.

Core components reference

StateSpaceSet{D, T, V} <: AbstractVector{V}

DynamicalSystem

Dynamical system implementations

DeterministicIteratedMap <: DiscreteTimeDynamicalSystem
DeterministicIteratedMap(f, u0, p = nothing; t0 = 0)

CoupledODEs <: ContinuousTimeDynamicalSystem
CoupledODEs(f, u0 [, p]; diffeq, t0 = 0.0)

StroboscopicMap <: DiscreteTimeDynamicalSystem
StroboscopicMap(ds::CoupledODEs, period::Real) → smap
StroboscopicMap(period::Real, f, u0, p = nothing; kwargs...)

StroboscopicMap(T::Real, f, u0, p = nothing; diffeq, t0 = 0) → smap

PoincareMap <: DiscreteTimeDynamicalSystem
PoincareMap(ds::CoupledODEs, plane; kwargs...) → pmap

using DynamicalSystemsBase, PredefinedDynamicalSystems
ds = Systems.rikitake(zeros(3); μ = 0.47, α = 1.0)
pmap = poincaremap(ds, (3, 0.0))
step!(pmap)
next_state_on_psos = current_state(pmap)

ProjectedDynamicalSystem <: DynamicalSystem
ProjectedDynamicalSystem(ds::DynamicalSystem, projection, complete_state)

ds = Systems.lorenz96(5)
projection = [4, 5]
complete_state = [0.0, 0.0, 0.0] # completed state just in the plane of last two dimensions
prods = ProjectedDynamicalSystem(ds, projection, complete_state)
reinit!(prods, [0.2, 0.4])
step!(prods)
current_state(prods)

ds = Systems.lorenz96(5)
projection(u) = [sum(u), sqrt(u[1]^2 + u[2]^2)]
complete_state(y) = repeat([y[1]/5], 5)
prods = # same as in above example...

ArbitrarySteppable <: DiscreteTimeDynamicalSystem
ArbitrarySteppable(
    model, step!, extract_state, extract_parameters, reset_model!;
    isdeterministic = true, set_state = reinit!,
)

reset_model!(model, u, p)

CoupledSDEs <: ContinuousTimeDynamicalSystem
CoupledSDEs(f, u0 [, p]; kwargs...)

(alg = SOSRA(), abstol = 1.0e-2, reltol = 1.0e-2)

Dynamical system interface

current_state(ds::DynamicalSystem) → u::AbstractArray

initial_state(ds::DynamicalSystem) → u0

observe_state(ds::DynamicalSystem, i, u = current_state(ds)) → x::Real

state_name(index)::String

current_parameters(ds::DynamicalSystem) → p

current_parameter(ds::DynamicalSystem, index [,p])

parameter_name(index)::String

initial_parameters(ds::DynamicalSystem) → p0

isdeterministic(ds::DynamicalSystem) → true/false

isdiscretetime(ds::DynamicalSystem) → true/false

dynamic_rule(ds::DynamicalSystem) → f

current_time(ds::DynamicalSystem) → t

initial_time(ds::DynamicalSystem) → t0

isinplace(ds::DynamicalSystem) → true/false

successful_step(ds::DynamicalSystem) -> true/false

referrenced_sciml_model(ds::DynamicalSystem)

Learn more

To learn more, you need to visit the documentation pages of the modules that compose DynamicalSystems.jl. See the contents page for more!