decompose([t, ] s, method::Decomposition) → x, r

Decompose an 1D input signal or timeseries s(t) into components, x, r, using the given method. t defaults to 1:length(s).

What are x and r really depends on your point of view and your application. They can be structure x and noise r (i.e. noise reduction). They can be seasonal/periodic x and residual component r. They can even be multiplier x and input r.

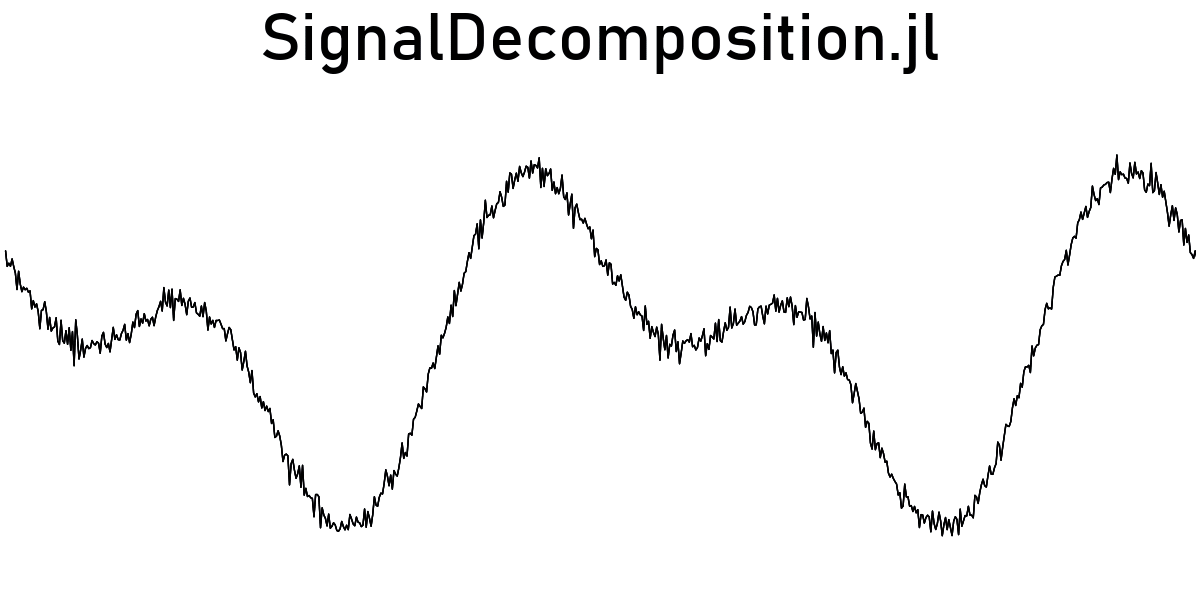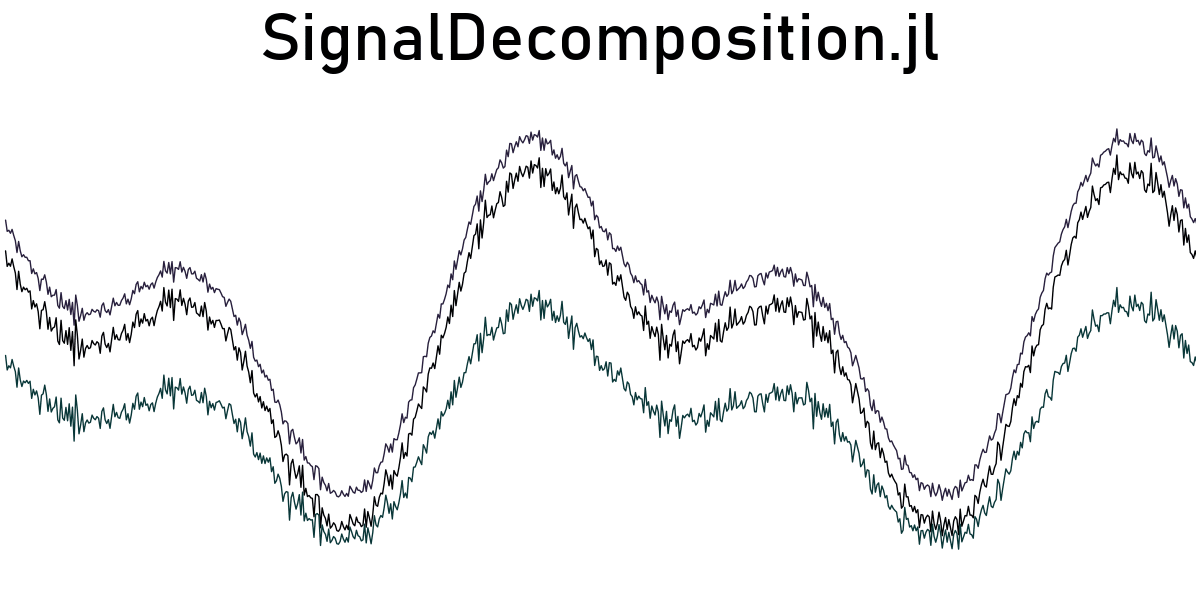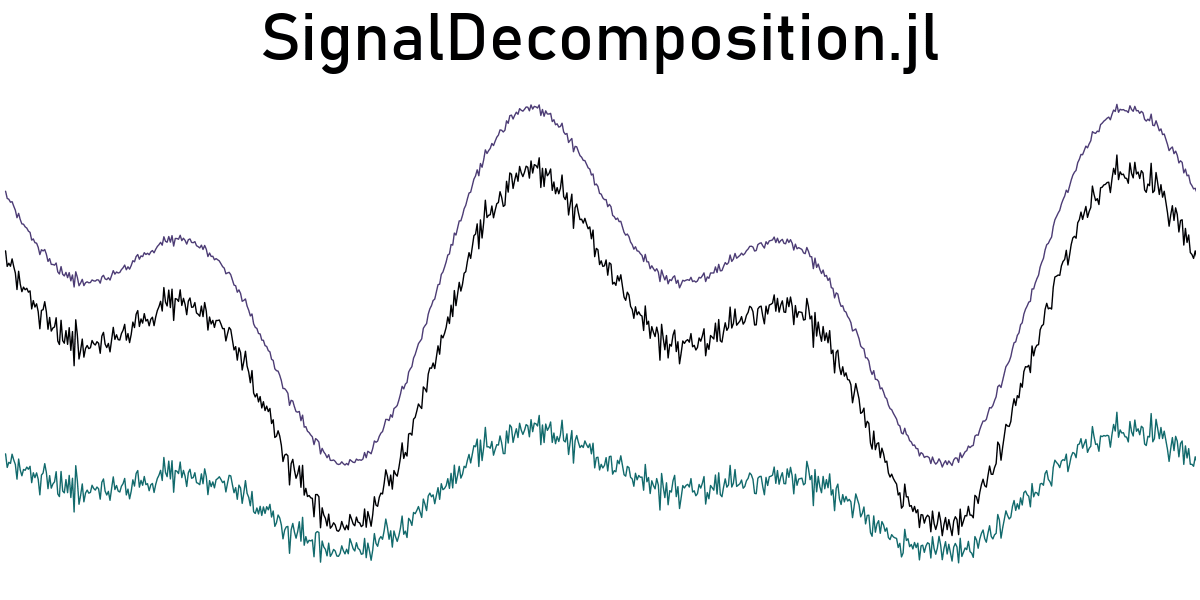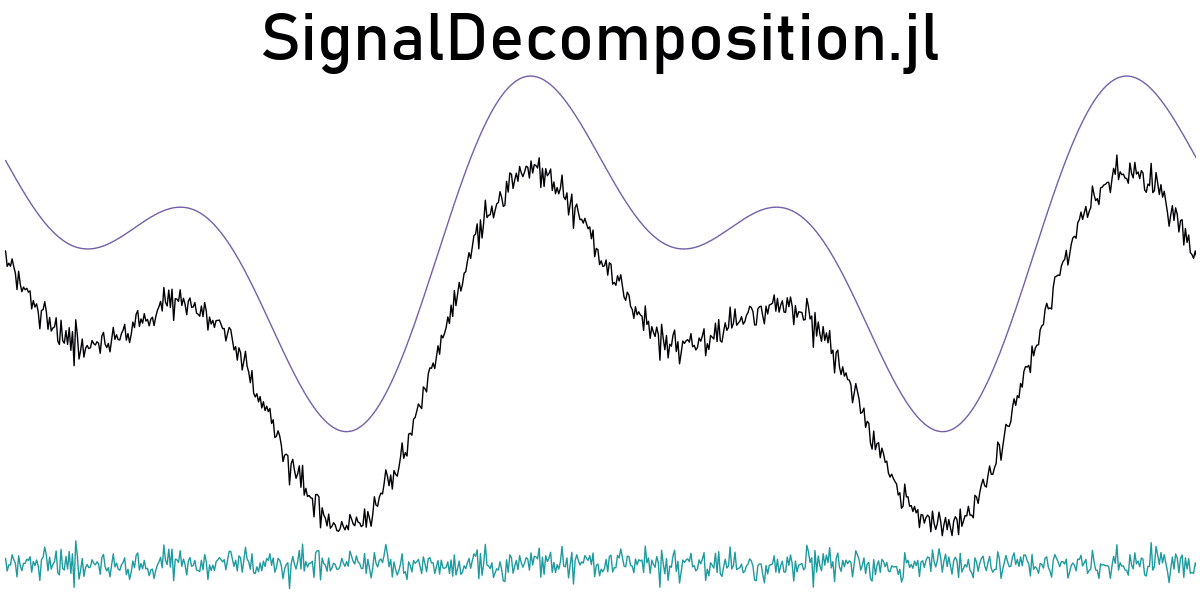
Fourier([s, ] frequencies, x=true) <: Decomposition

Decompose a timeseries s into a sum x + r, by identifying specific frequencies at the Fourier space and removing them from the signal. x is the removed periodic component while r is the residual. If a given frequency is not exactly matching the Fourier frequencies, the closest one is removed.

Important: periods/frequencies are defined with respect to the t axis length, the actual t values are not used in this method. So, frequency 1/12 (a period of 12) means 12 data points (whose actual value depends on t).

If you provide s the method plans the forward and inverse Fourier transforms (so that it is efficient to re-use it for s of same type and length).

This method works well when a periodic signal P is superimposed on fluctuations S, and you have a good educated guess of what frequencies compose P. This method works well if the given signal has length multiple of the periods given.

There is arbitrarity of which part of the signal x, r gets the mean value of s, because it is deducted for a better fit. The argument x=true attributes it to x, use false for r.

FrequencySplit([s, ] f::Real) <: Decomposition

Similar to the Fourier method, but now the "residual" signal is the part of s with frequencies higher than f, while the "seasonal" part has frequencies ≤ f.

Sinusoidal(fs)

Decompose a timeseries s into a sum x + r, where x are sinusoidal components with the given frequencies fs that minimize coefficients $A, \phi$ of the expression

\[s \approx A_0 + \sum_i A_i \cos(2\pi f_i t + \phi_i)\]

with $A_0 = \bar{s}$ the mean.

This method uses a new least-squares algorithm in frequency domain using the package LPVSpectral.jl, see^[Bagge2017]. It works for non-equispaced t axis (and also normal), is generally very accurate (if choosen frequencies are not too close), but has performance scaling of O(N^2.4) instead of O(n log(n)) of Fourier.

Because it can work with arbitrary signal length the method always estimates the zero-frequency Fourier component, and attributes it to x. The fitted coefficients $A, \phi$ are available as fields .A and .φ of the struct (first entry is zero-frequency component $A_0, \phi_0$).

ExtremelySimpleNL(k::Int, ℓ::Int, w::Int, τ::Int, ε::Real) <: Decomposition

Quite literally the "extremely simple nonlinear noise-reduction method"^{[Schreiber1993]}. It decomposes s into the sum x + r with x being the "noiseless" timeseries. This is the average position of neighbors in the delay embedded space.

This method works well if your timeseries is composed by the addition of a structured component (which follows deterministic and stationary dynamics which the embedding should approximate) and some noise.

The cited paper has some info on choosing optimal ε.

Arguments:

• k amount of past delay
• ℓ amount of forward delay
• w Theiler window
• τ delay time
• ε radius of the neighborhood in the embedded space

ManifoldProjection(m, Q, k, τ=1, w=0, r=1000.0) <: Decomposition

A nonlinear noise reduction method, also known as "locally linear projections", which works by bringing a noisy signal closer to a multi-dimensional manifold that represents the deterministic dynamics of the signal. The method is method "IV" of ^{[Grassberger1993]}.

m::Int is the same as in ^{[Grassberger1993]}, the embedding dimension. Q is related with the expected dimension d of the manifold of the deterministic with approximate relation d ≈ m-Q+1. However, it is best t consider Q as an input parameter (the dimension of the set you project locally into) and you need to vary it to achieve the best performance. If given a Vector{Int} as Q the algorithm will iteratively do noise reduction to the resulting outputs (thus a vector is strongly recommended). Duplicate entries can exist in Q.

k can be either Int or a SearchType from Neighborhood.jl. If Int, the k nearest neighbors are choosen as the neighborhood 𝓤 of each point. The paper contains an involved process for determining optimal k::Int, see eq.(5.4). w is just the Theiler window, while r is the value of the edge entries of vector R, and probably has not much impact (the rest of the entries are 1).

In the paper too big correction vectors were rescaled to the average magnitude of corrections, using as a criterion the distribution of their size. This is not implemented here (as it is not clear exactly what it means computationally, what is "too big"?) Contributing it is welcomed if you know how...

See also ^{[Schreiber1996]} for an application of the same algorithm in real ECG data.

ProductInversion(r, μ; verbose=false) <: Decomposition

Decompose a timeseries s into a product x * r, given that you have a good estimate of the second factor r (the "input") and you need x (the "multiplier") but you can't do simply x = s ./ r because r contains zeros.

This method works well when the characteristic timescales of x are comparable, or larger than those of r but not much smaller.

The second argument μ is a regularization parameter. In short, we estimate r by minimizing a cost with two components: that x is close to s/r and that x is smooth. μ is the multiplier of the smoothness cost.

You can give a vector as μ. The process will be repeated for all μ and the rmse between s and the estimated x * r will be computed. The x that gives the least error will be returned finally. If verbose = true, the method also prints the pairs (μ, err) for each μ.

Use the low level SignalDecomposition.matrix_invert(s, r, μ::Real) → x, err to get the error values.

TimeAnomaly()

Decompose timeseries s into a sum x + r wher x is the same-time average and r is the anomalies. Each unique day+month combination in t is identified, and the values of s for each year that has this day+month combination are averaged. As a result, the time vector t must be <:AbstractVector{<:TimeType}.

This method is very common in climate science, referred to as simply "anomalies".

rmse(x, y) → e

Return the root mean square error e of the "fit" y into data x.

nrmse(x, y) → e

Return the normalized root mean square error of the "fit" y into data x. This number is the relative error of y to x versus mean(x) to x, i.e. if e < 1 the fit y is better than using mean(x) as a fit.

σrmse(x, y) = rmse(x, y)/std(x)

Relative error of the fit y to data x with respect to std(x).