Fourier surrogates (FS)
Fourier surrogates are a form of constrained surrogates created by taking the Fourier transform of a time series, then shuffling either the phase angles or the amplitudes of the resulting complex numbers. Then, we take the inverse Fourier transform, yielding a surrogate time series.
Random phase surrogates
TimeseriesSurrogates.randomphases — Function.randomphases(ts)Create a random phases surrogate for ts [1]. Surrogate realizations using the phase surrogates have the same linear correlation, or periodogram, as the original data.
ts Is the time series for which to generate an AAFT surrogate realization.
Literature references
J. Theiler et al., Physica D 58 (1992) 77-94 (1992).
Here's how you would generate a phase surrogate realization of a time series.
using TimeseriesSurrogates
# Generate a time series. This time, we'll use a NSAR2() process.
ts = NSAR2()
# Generate a random phase surrogate realization
surrogate = randomphases(ts)
# Plot the surrogate along with the time series it is based on, along with autocorrelation
# and periodogram plots.
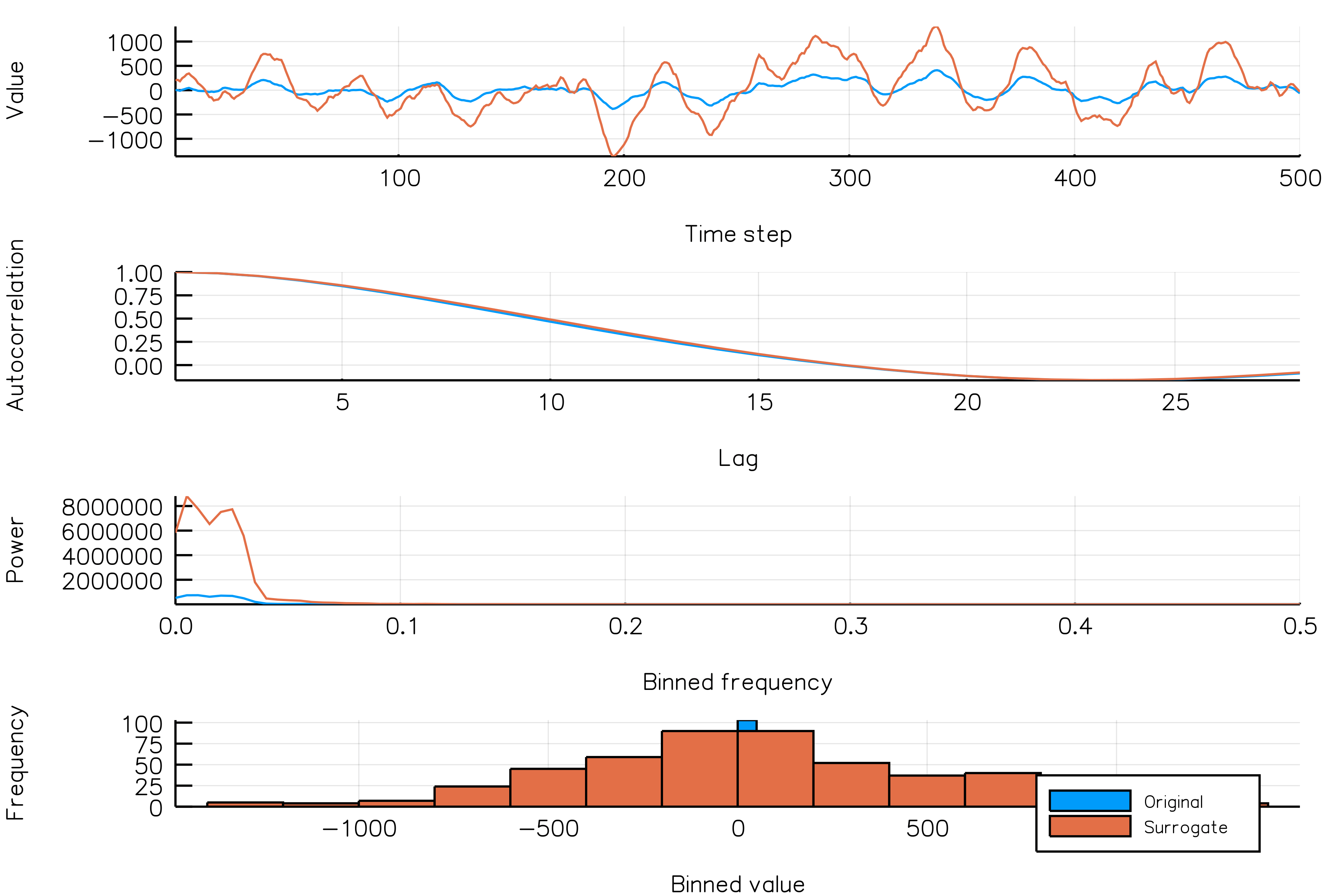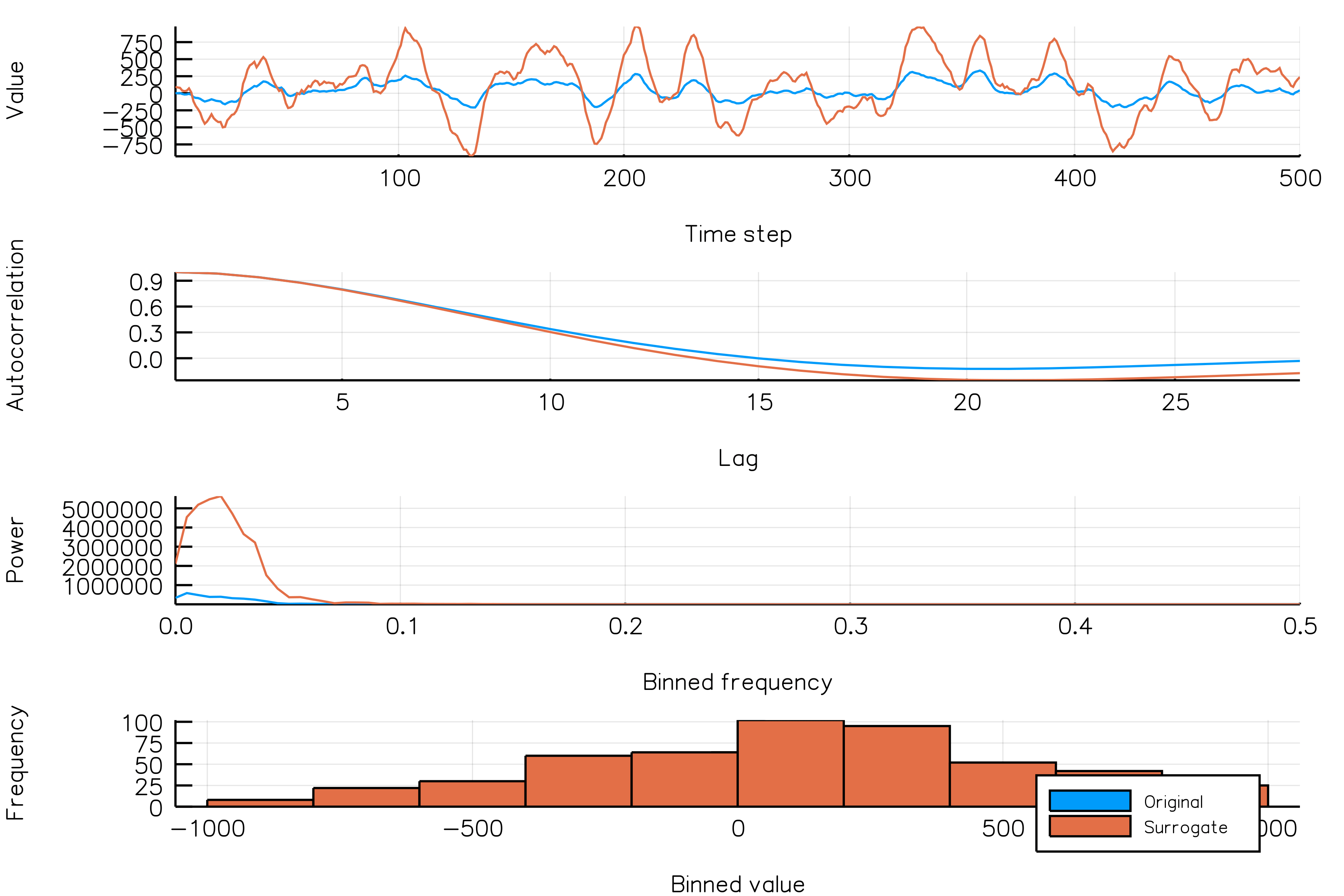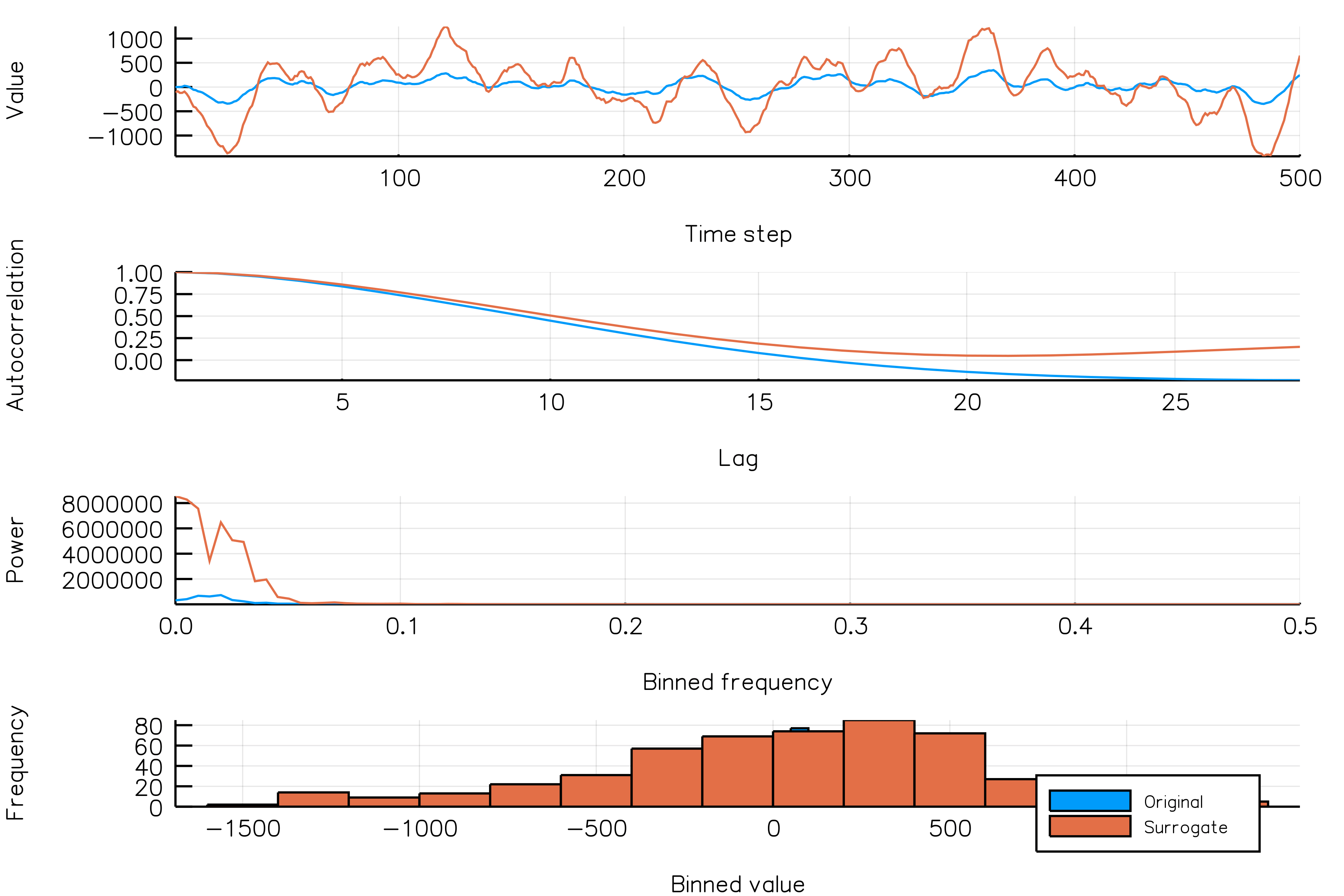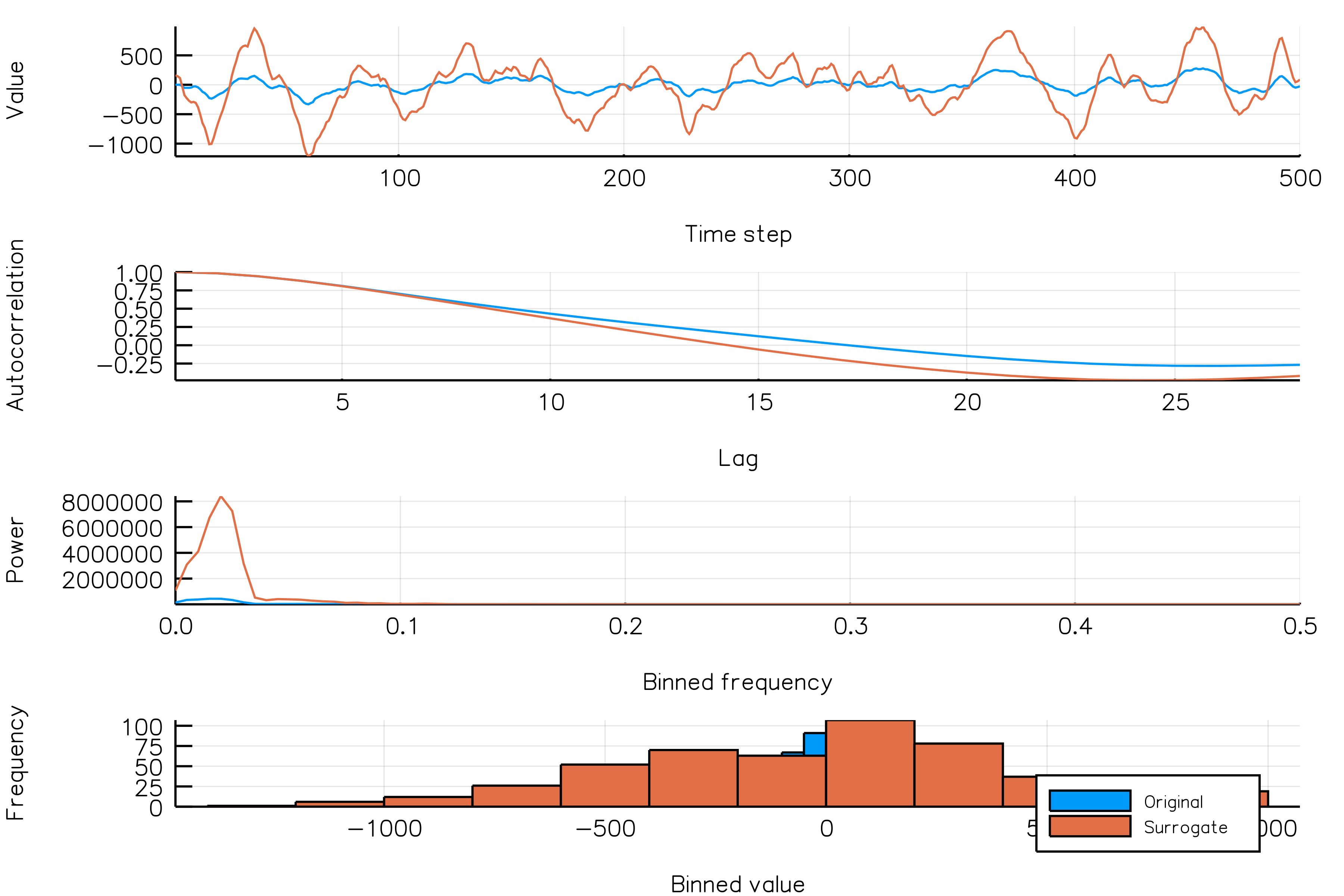
surrplot(ts, surrogate)How do random phase surrogates vary across realizations?
Below is a plot showing different phase surrogate realizations (orange) over the same time series (blue). Each frame in the animation is a different surrogate realization. Note that the autocorrelations are roughly similar across realizations.
randomphases_NSAR2_gif(n_iters = 30, fps = 5)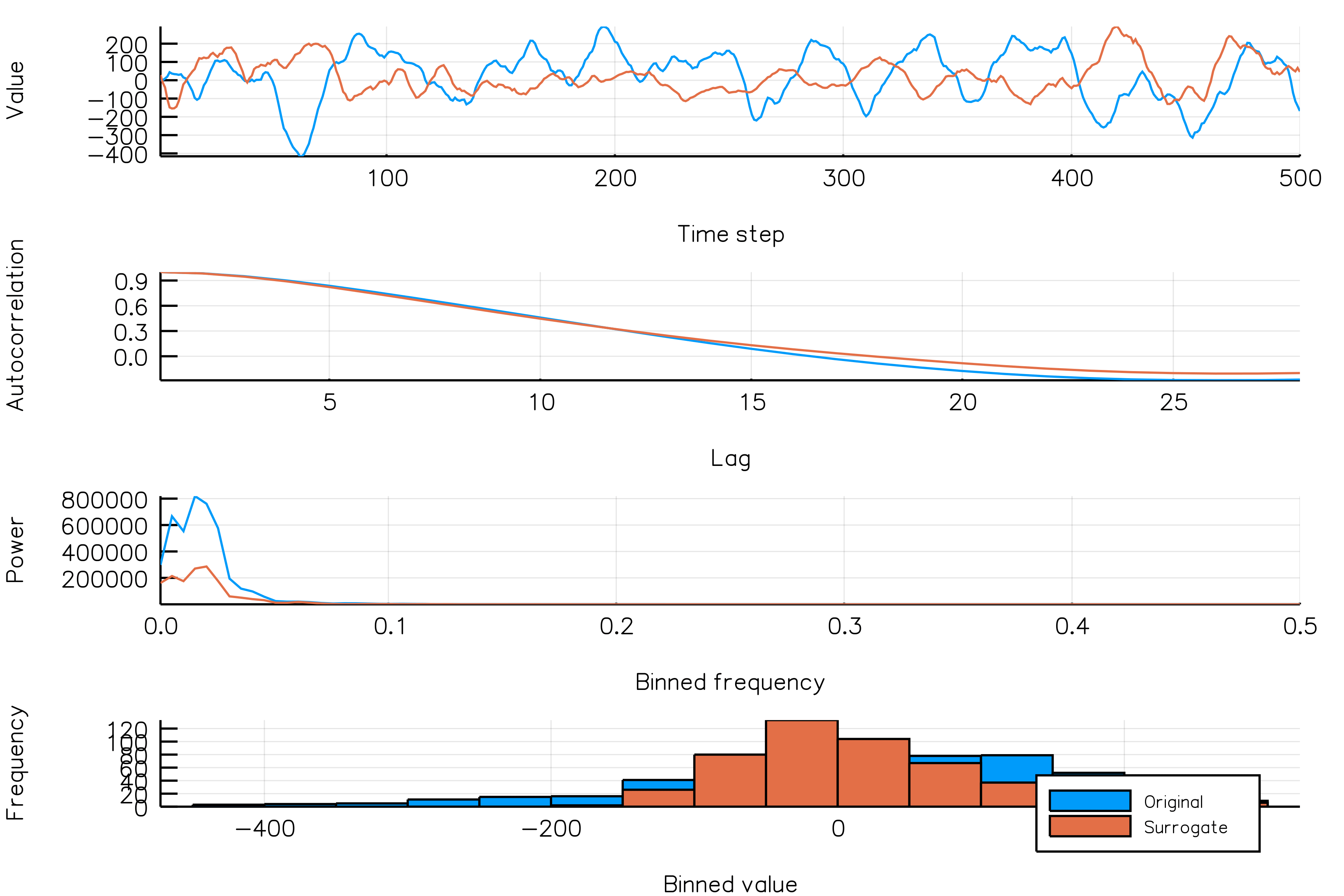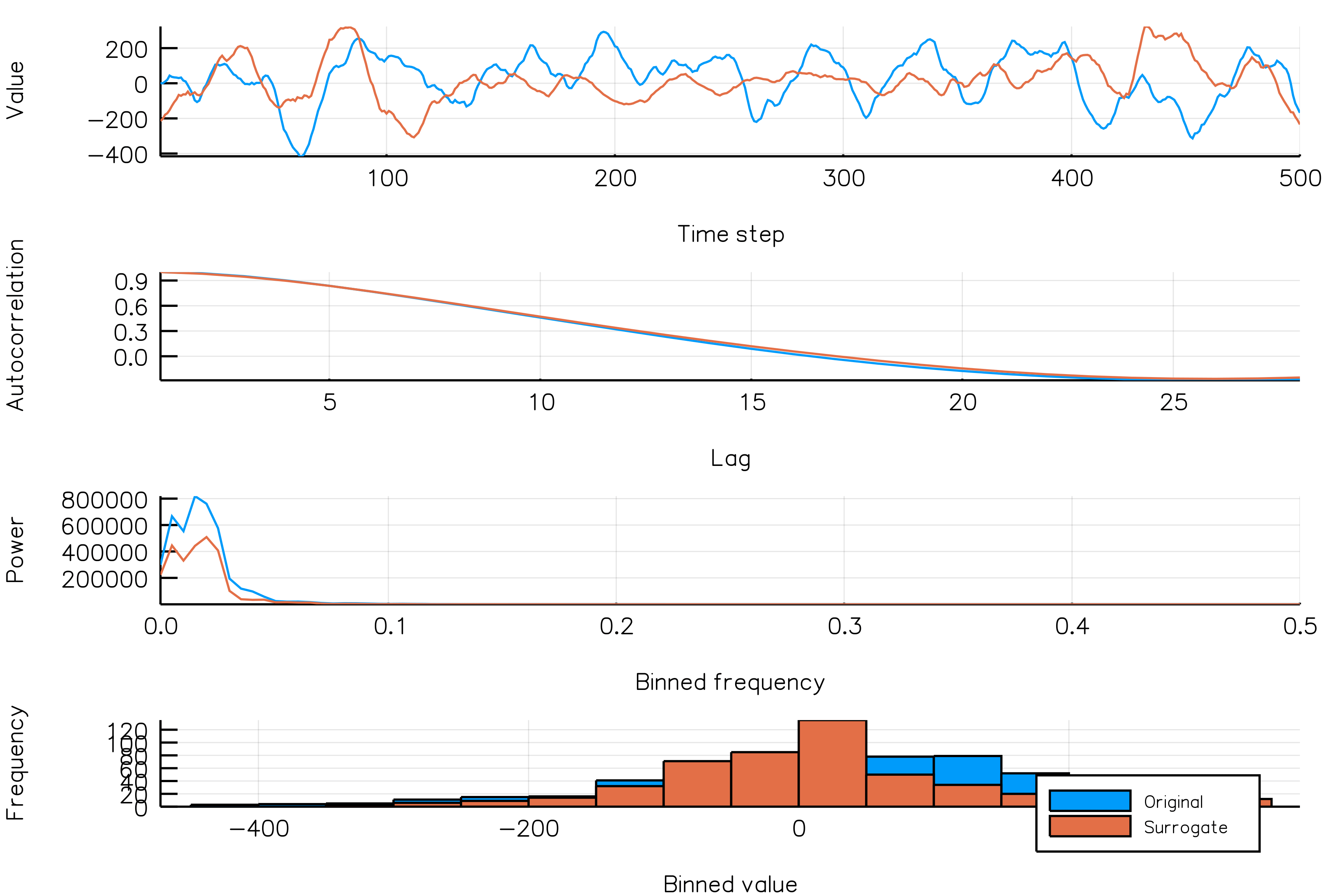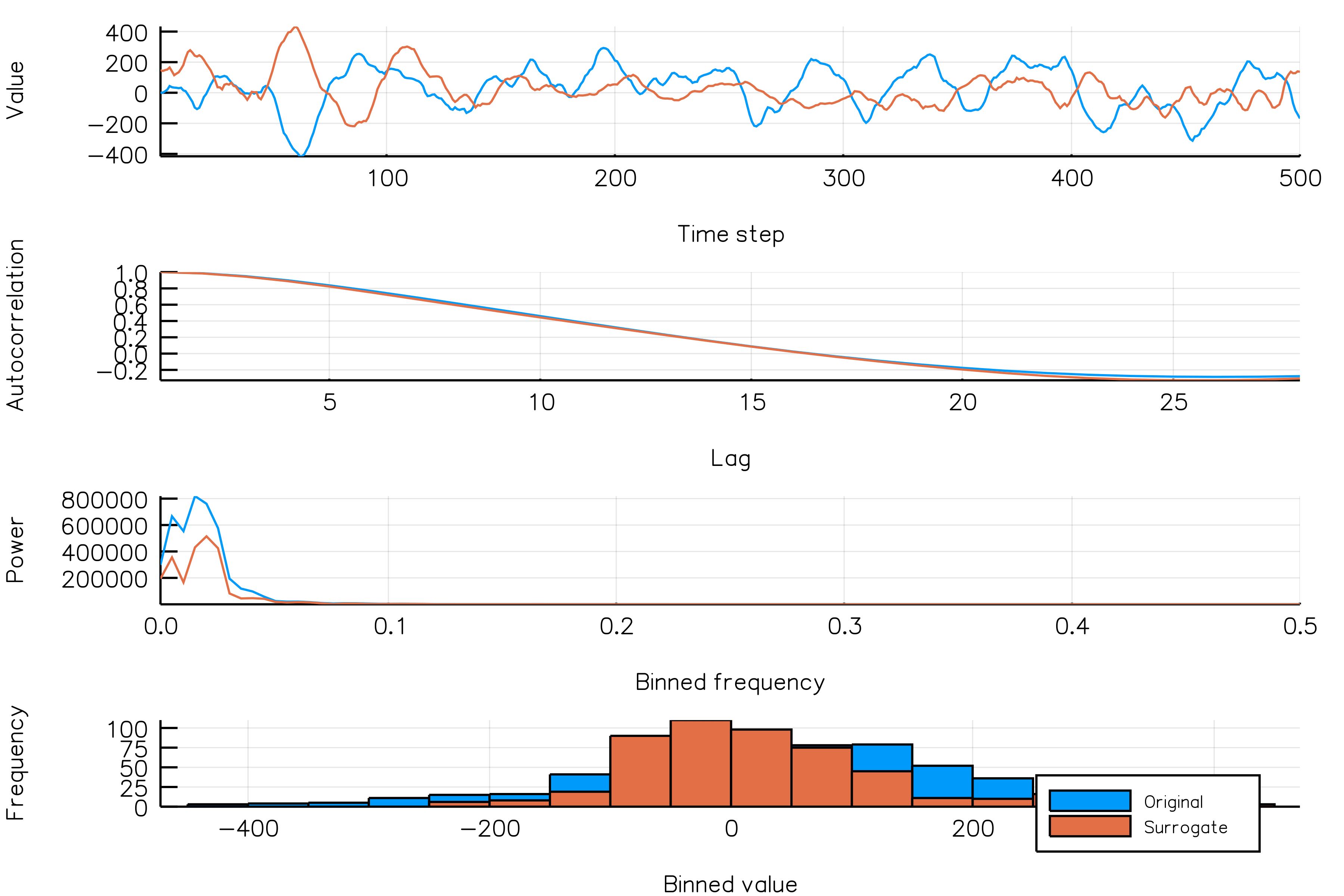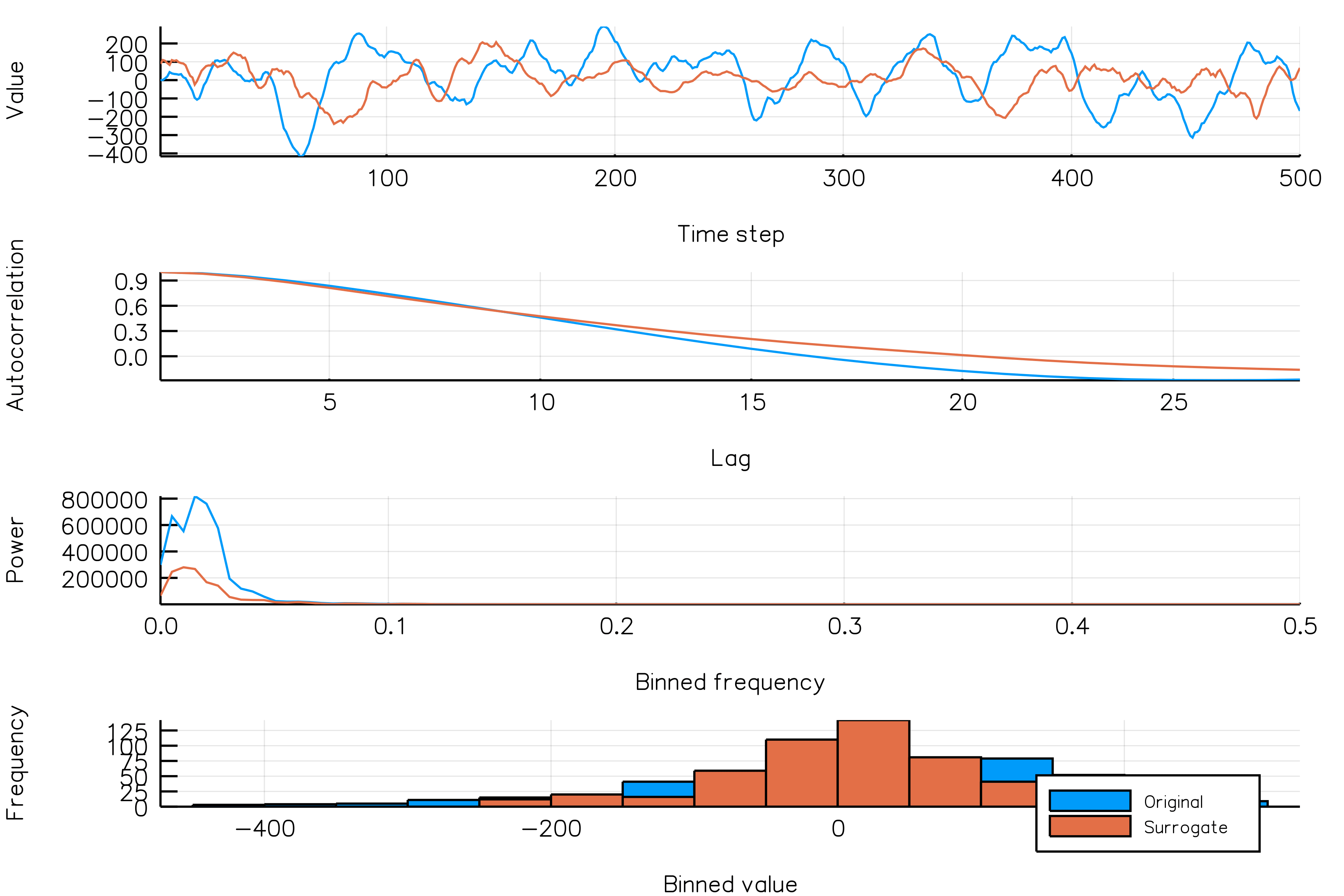
In the next animation, the time series (blue) for which we generate surrogates change between frames. One phase surrogate realization (orange) is generated for each of the time series. Notice that, again, the phase surrogates accurately represents the autocorrelation of the different initial time series.
randomphases_NSAR2_gif(n_iters = 30, fps = 5, new_realization_every_iter = true)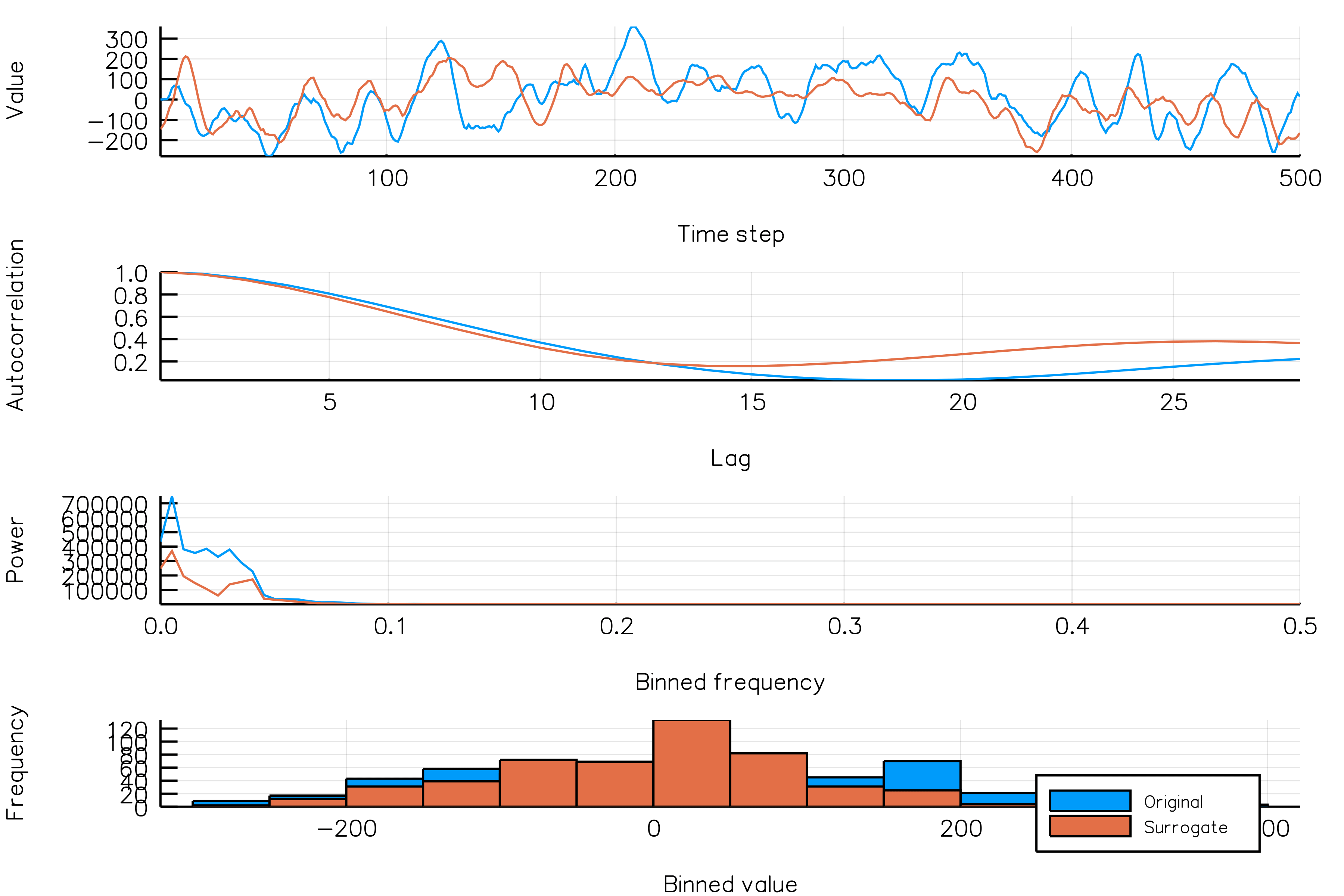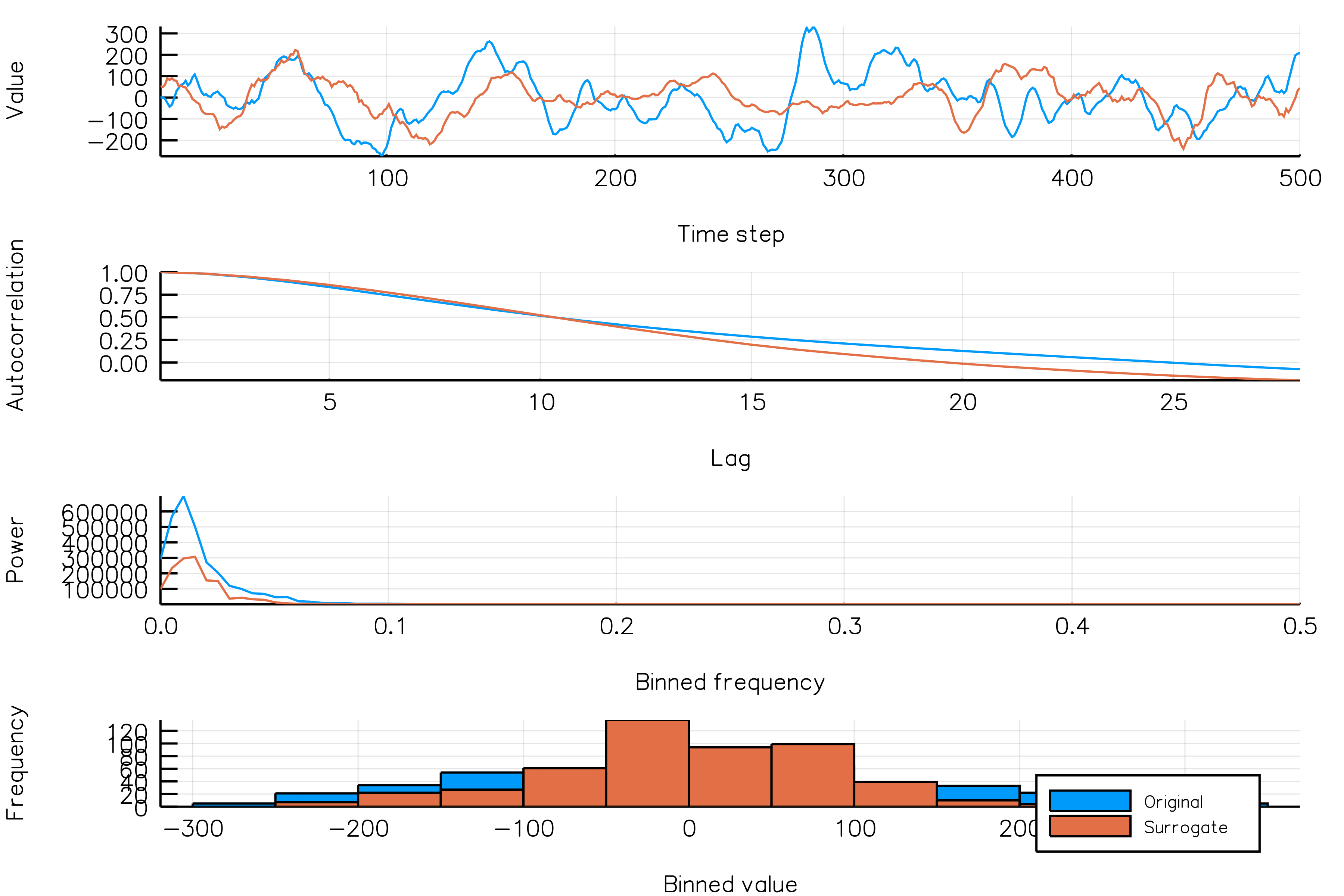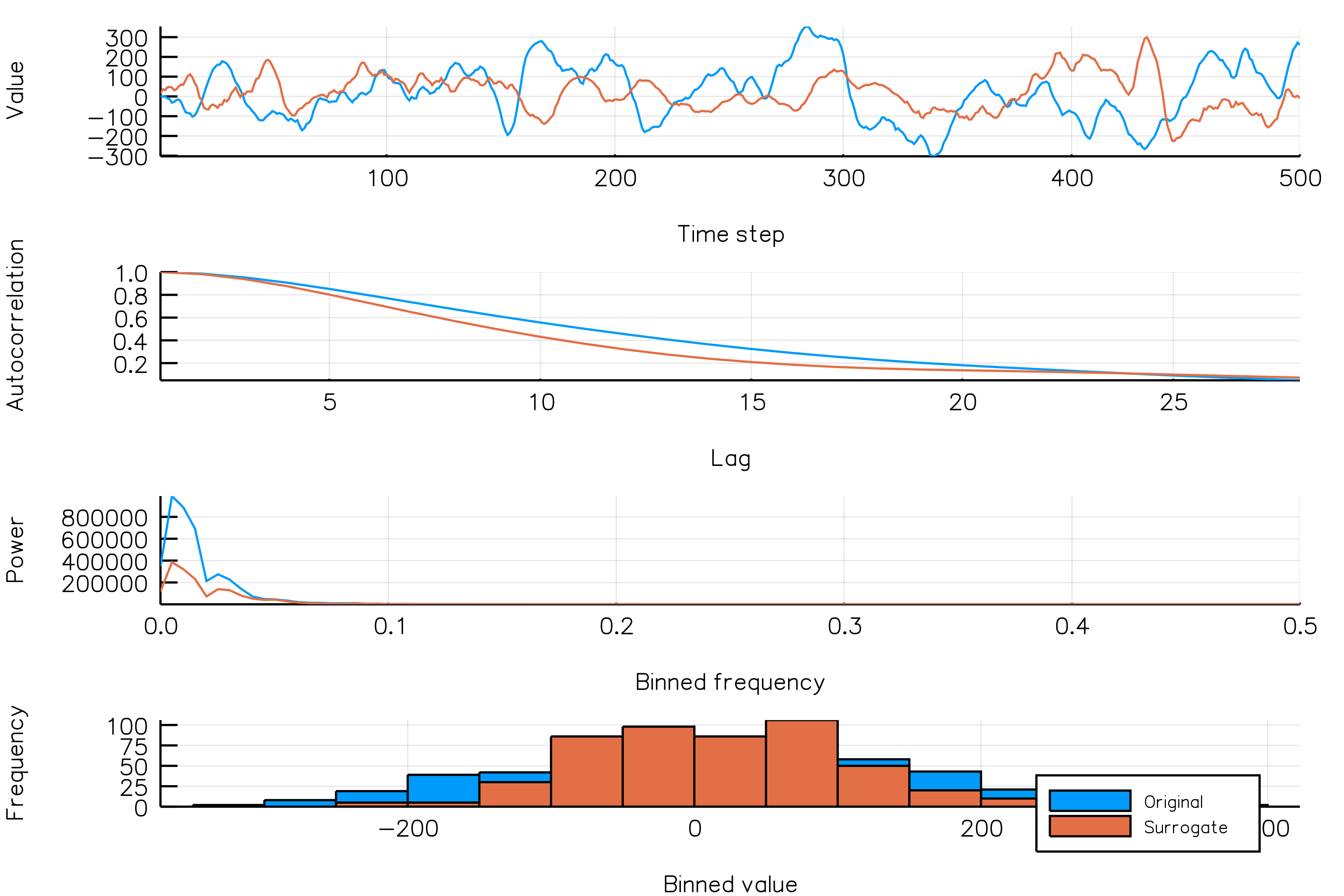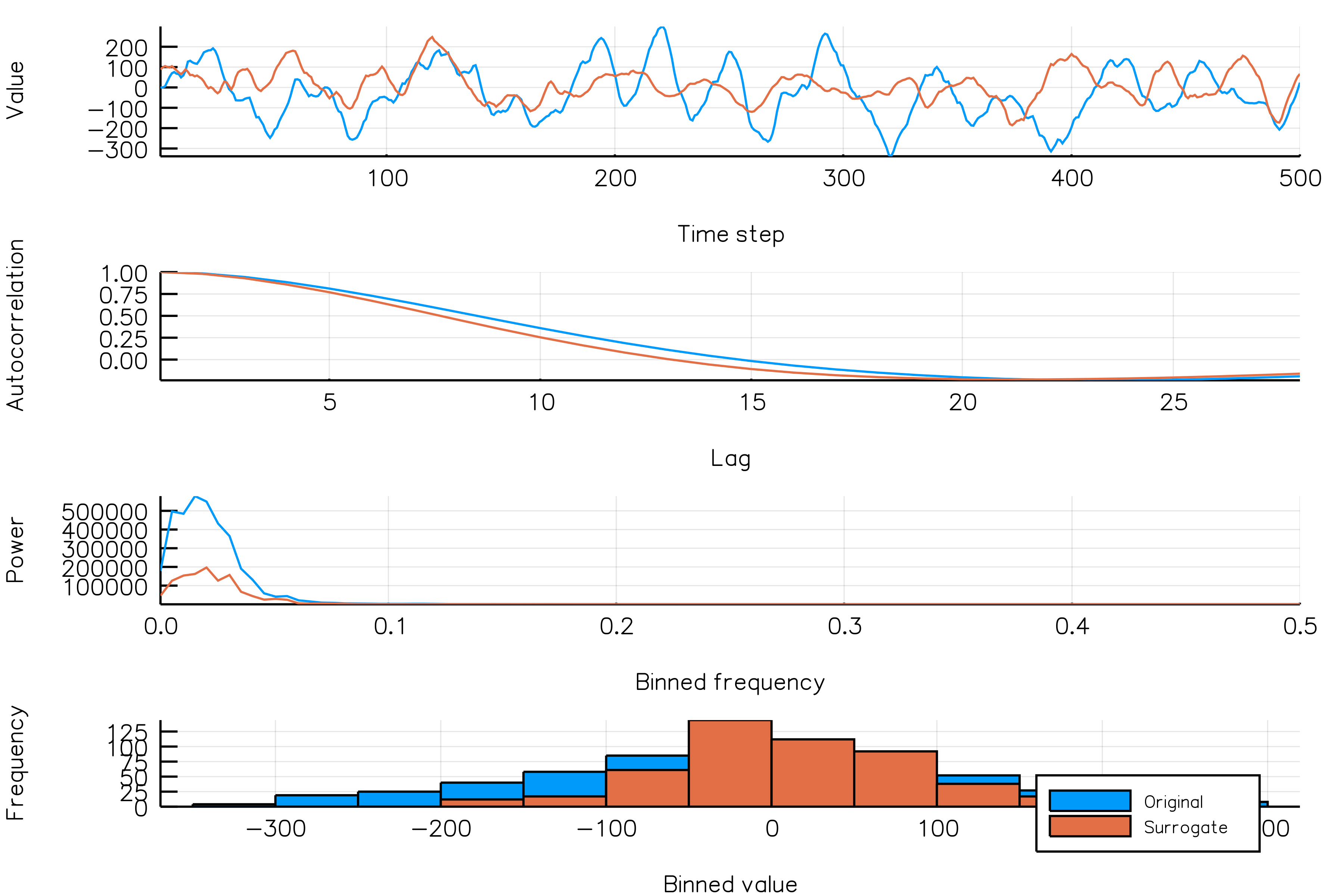
Random amplitude surrogates
TimeseriesSurrogates.randomamplitudes — Function.randomamplitudes(ts)Create a random amplitude surrogate for ts.
A modification of the random phases surrogates [1] where amplitudes are adjusted instead of the phases after taking the Fourier transform.
ts Is the time series for which to generate an AAFT surrogate realization.
Literature references
J. Theiler et al., Physica D 58 (1992) 77-94 (1992))
This is how you would generate a random amplitude surrogate realization of a time series.
using TimeseriesSurrogates
# Generate a time series. Again, we'll use a NSAR2() process.
ts = NSAR2()
# Generate a random amplitude surrogate realization
surrogate = randomamplitudes(ts)
# Plot the surrogate along with the time series it is based on, along with autocorrelation
# and periodogram plots.
surrplot(ts, surrogate)How do random amplitude surrogates vary across realizations?
Below is a plot showing different phase surrogate realizations (orange) over the same time series (blue).
randomamplitudes_NSAR2_gif(n_iters = 30, fps = 5)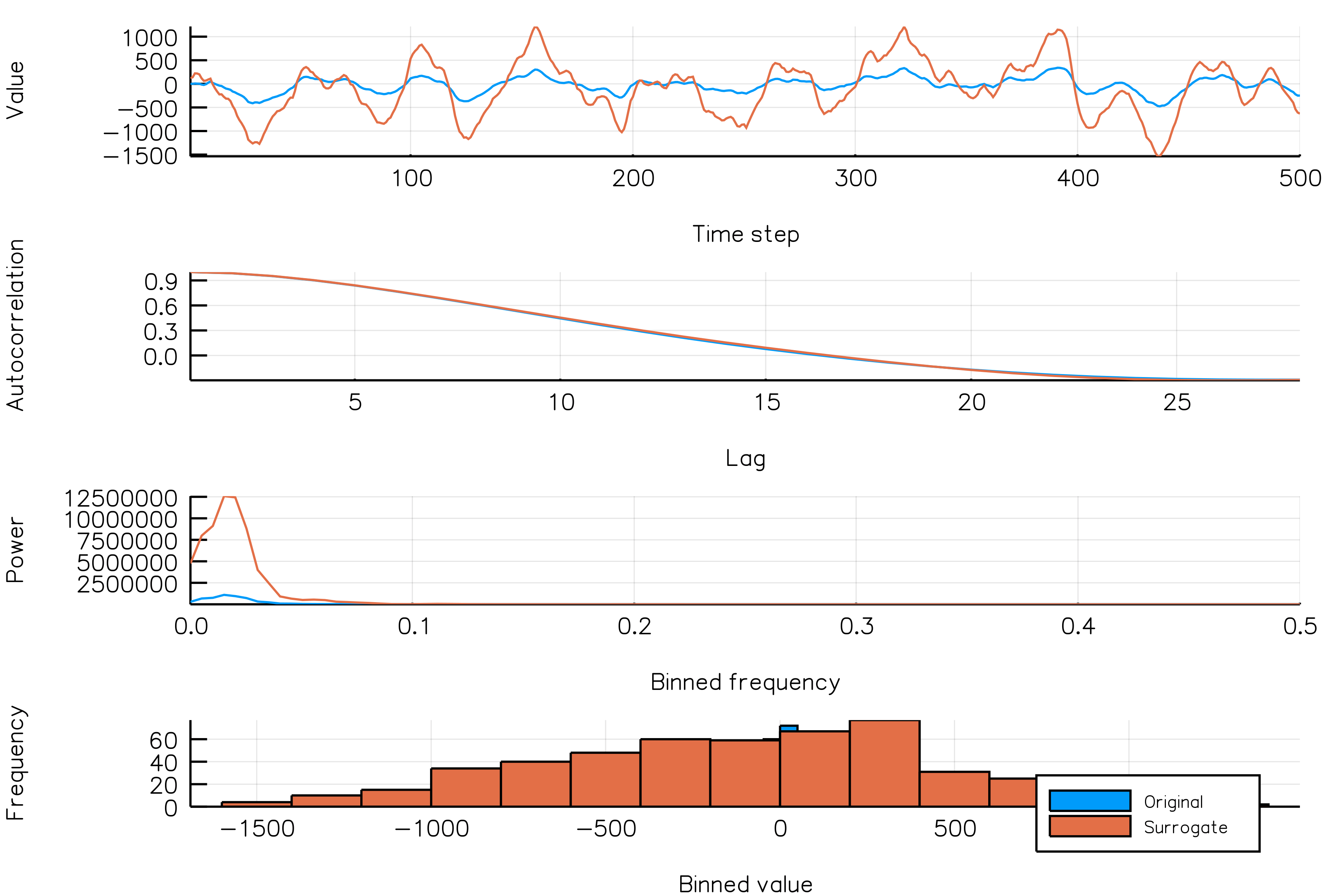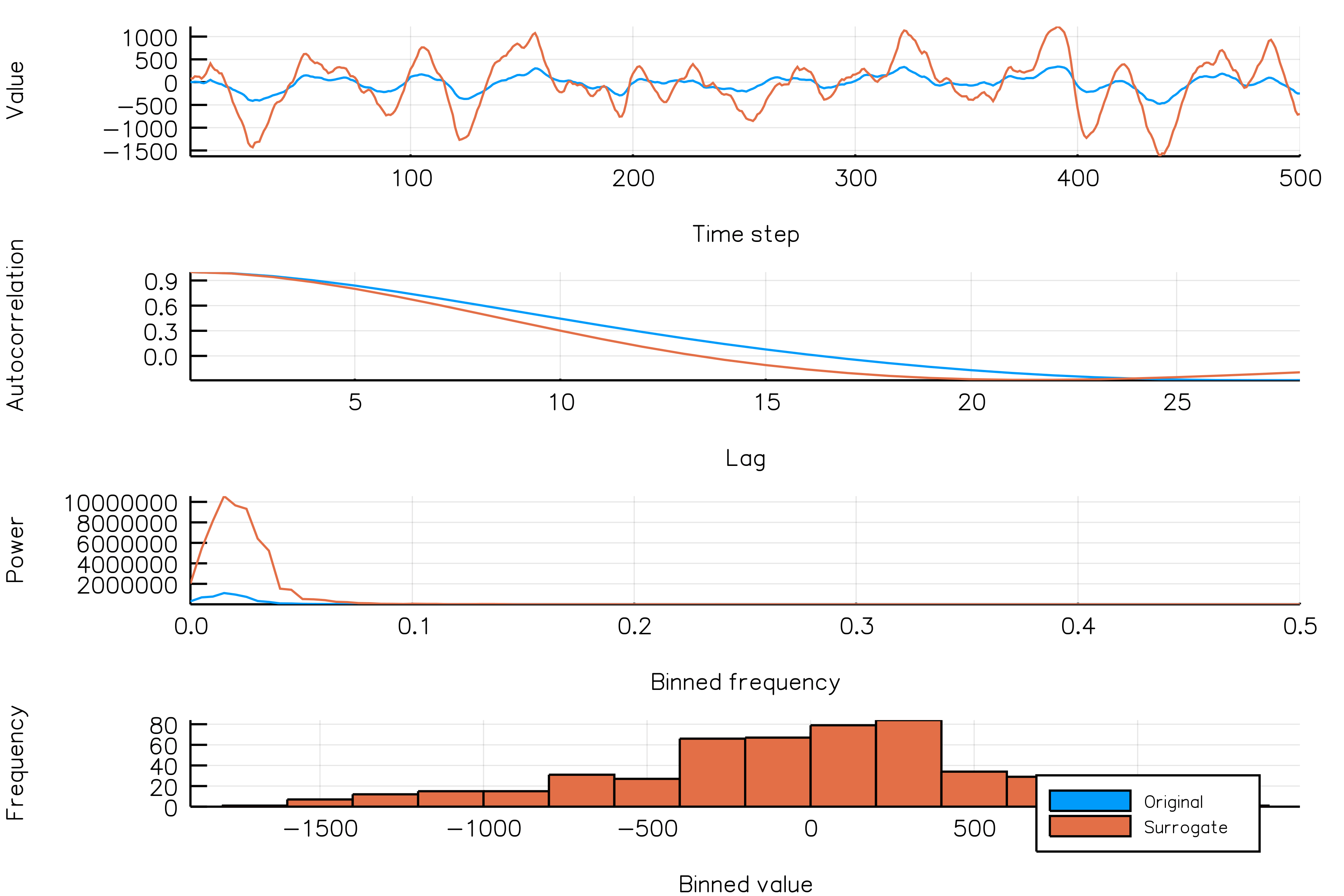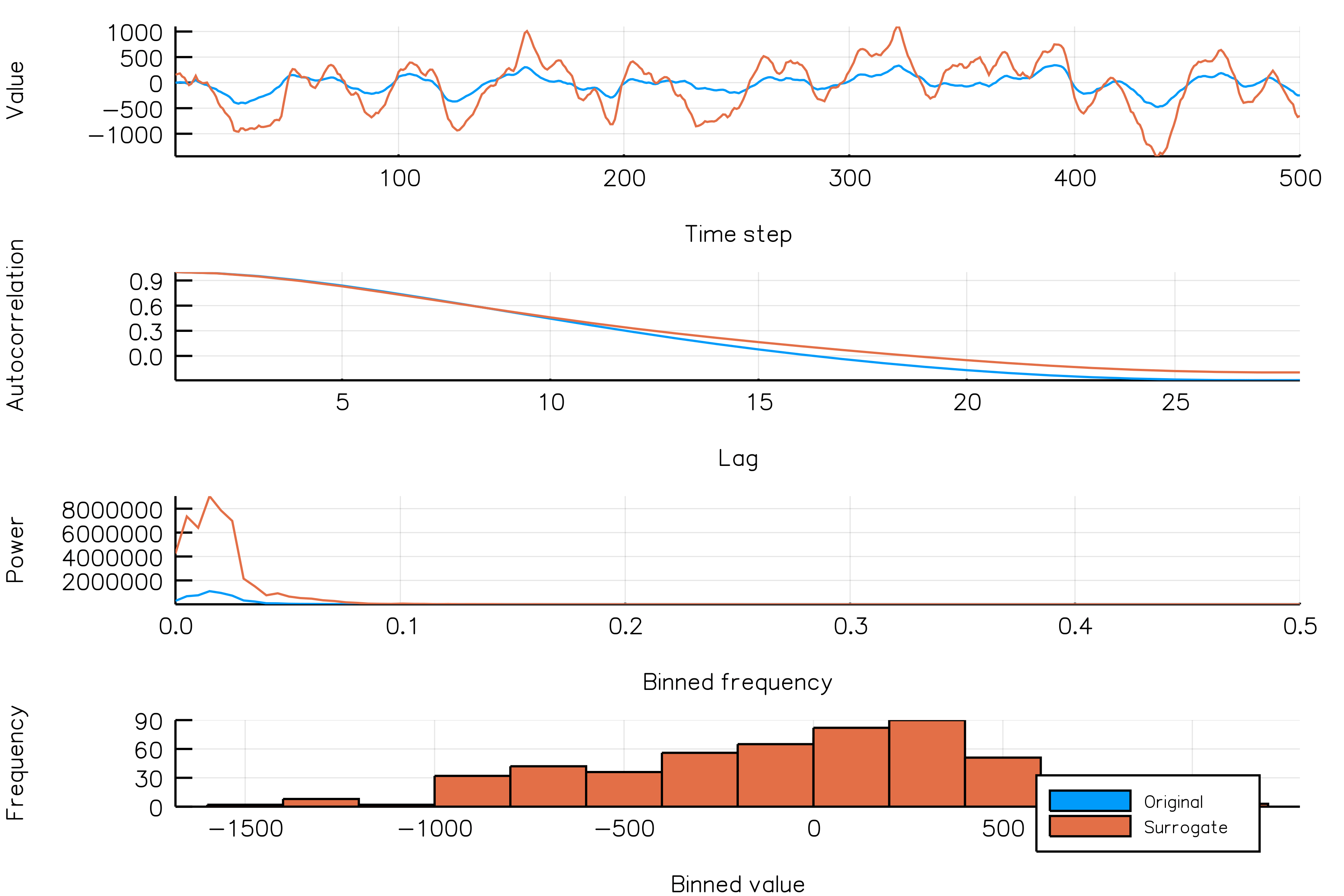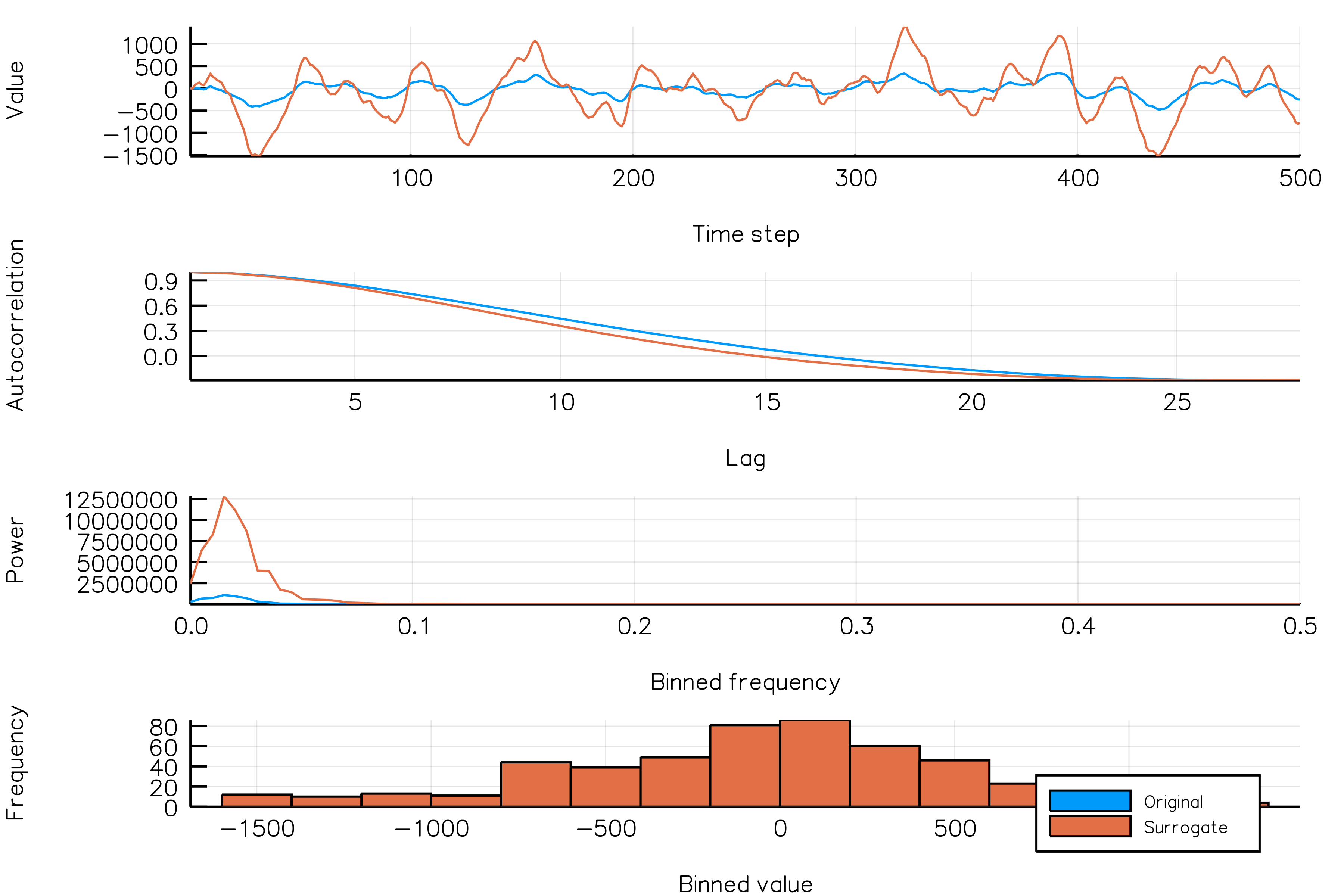
In the next animation, as above, each frame shows a new time series (blue), which every frame is another unique realization of the NSAR2 process, and one surrogate realization of the time series (orange).
randomamplitudes_NSAR2_gif(n_iters = 30, fps = 5,
new_realization_every_iter = true)