Surrogates for nonstationary time series
Several of the methods provided by TimeseriesSurrogates.jl can be used to construct surrogates for nonstationary time series, which the following examples illustrate.
Truncated Fourier surrogates
TFTS
By retaining the lowermost frequencies of the frequency spectrum, (TFTS) surrogates preserve long-term trends in the signals.
using TimeseriesSurrogates
n = 300; a = 0.7; A = 20; σ = 15
x = cumsum(randn(n)) .+ [(1 + a*i) .+ A*sin(2π/10*i) for i = 1:n] .+
[A^2*sin(2π/2*i + π) for i = 1:n] .+ σ .* rand(n).^2;
# Preserve 5 % lowermost frequencies.
surroplot(x, surrogate(x, TFTS(0.05)))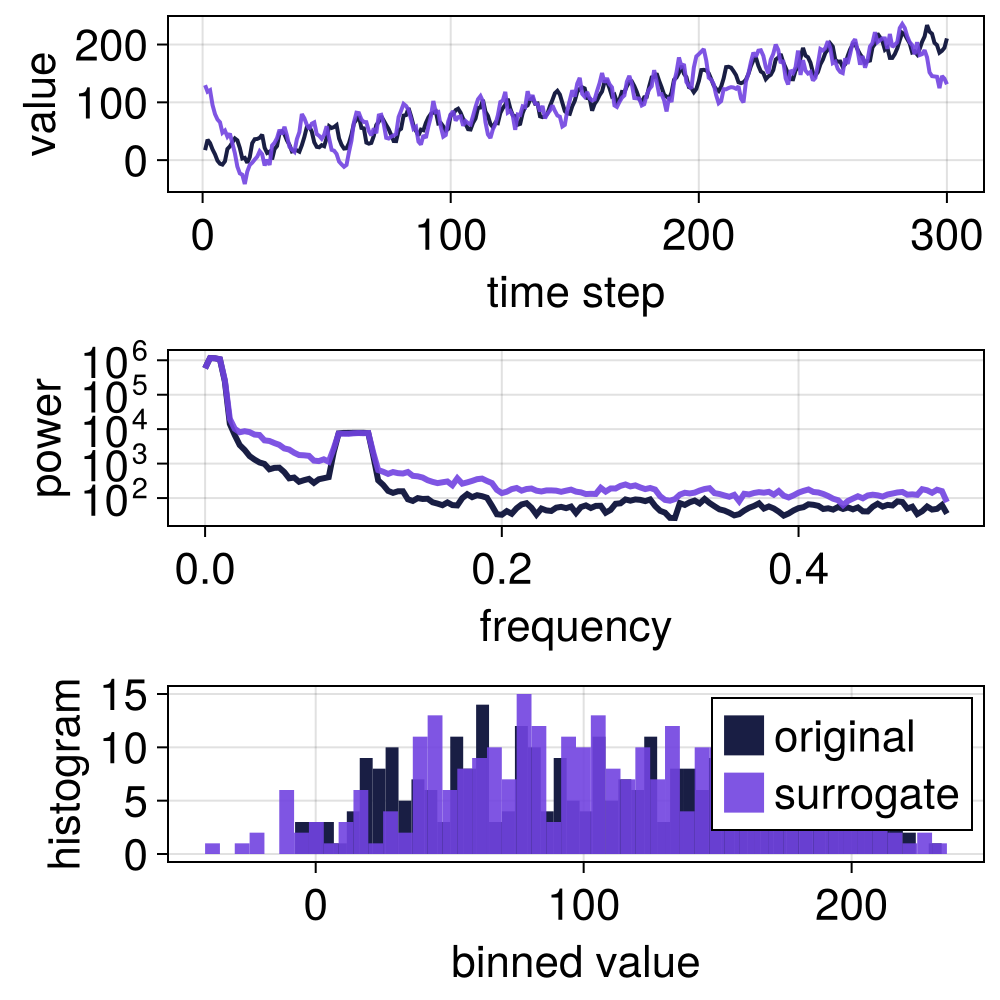
TAAFT
Truncated AAFT surrogates (TAAFT) are similar to TFTS surrogates, but also rescales back to the original values of the signal, so that the original signal and the surrogates consists of the same values. This, however, may introduce some bias, as demonstrated below.
using TimeseriesSurrogates
# Example signal
n = 300; a = 0.7; A = 20; σ = 15
x = cumsum(randn(n)) .+ [(1 + a*i) .+ A*sin(2π/10*i) for i = 1:n] .+
[A^2*sin(2π/2*i + π) for i = 1:n] .+ σ .* rand(n).^2;
# Preserve 5% of the power spectrum corresponding to the lowest frequencies
s_taaft_lo = surrogate(x, TAAFT(0.05))
surroplot(x, s_taaft_lo)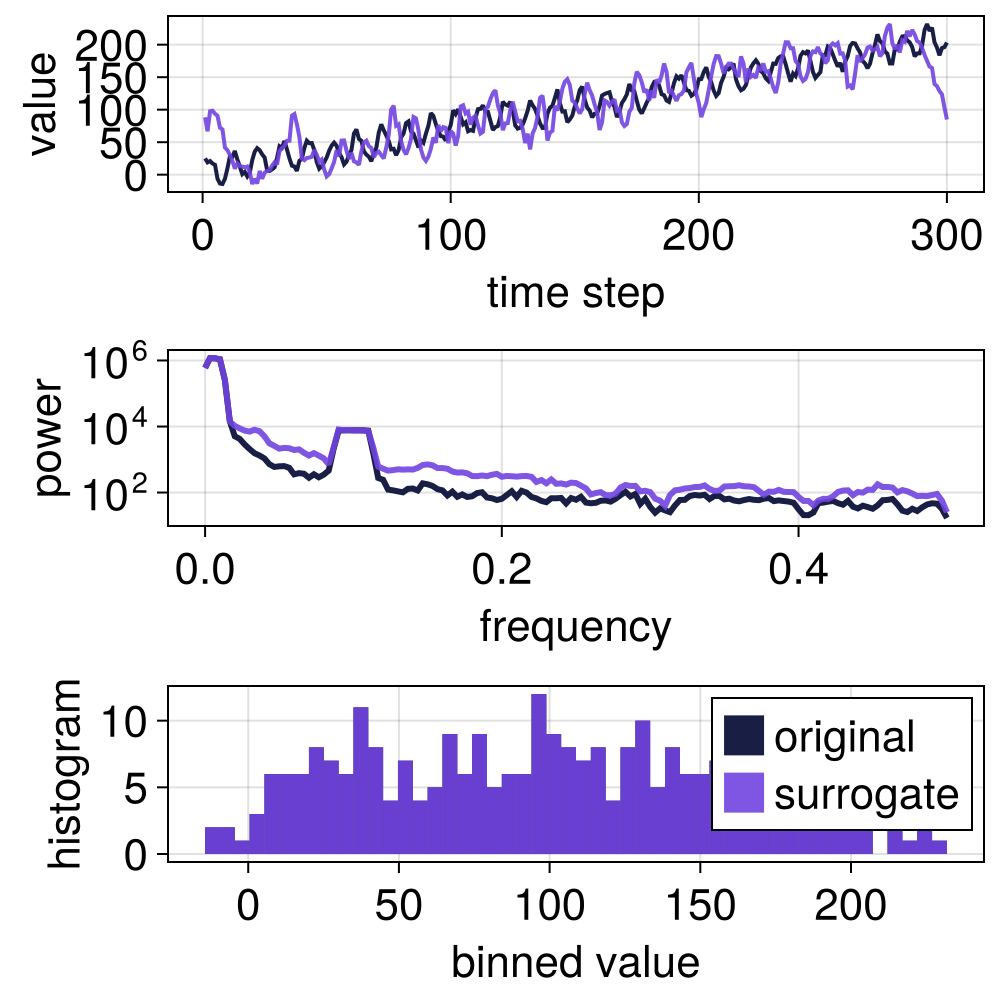
using TimeseriesSurrogates
# Example signal
n = 300; a = 0.7; A = 20; σ = 15
x = cumsum(randn(n)) .+ [(1 + a*i) .+ A*sin(2π/10*i) for i = 1:n] .+
[A^2*sin(2π/2*i + π) for i = 1:n] .+ σ .* rand(n).^2;
# Preserve 20% of the power spectrum corresponding to the highest frequencies
s_taaft_hi = surrogate(x, TAAFT(-0.2))
surroplot(x, s_taaft_hi)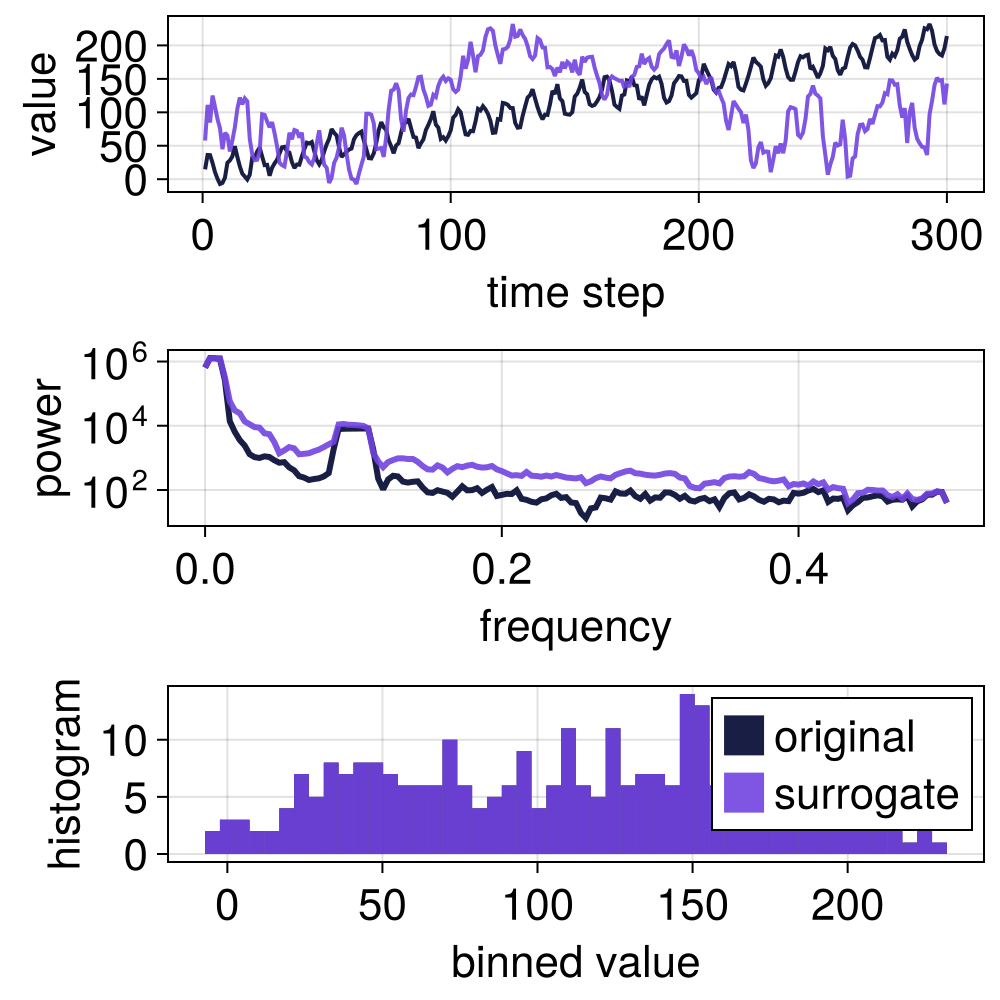
Truncated FT surrogates with trend removal/addition
One solution is to combine truncated Fourier surrogates with detrending/retrending. For time series with strong trends, Lucio et al. (2012)[Lucio2012] proposes variants of the truncated Fourier-based surrogates wherein the trend is removed prior to surrogate generation, and then added to the surrogate again after it has been generated. This yields surrogates quite similar to those obtained when using truncated Fourier surrogates (e.g. TFTS), but reducing the effects of endpoint mismatch that affects regular truncated Fourier transform based surrogates.
In principle, any trend could be removed/added to the signal. For now, the only option is to remove a best-fit linear trend obtained by ordinary least squares regression.
TFTD
The TFTD surrogate is a random Fourier surrogate where the lowest frequencies are preserved during surrogate generation, and a linear trend is removed during preprosessing and added again after the surrogate has been generated. The TFTD surrogates do a decent job at preserving long term trends.
using TimeseriesSurrogates
# Example signal
n = 300; a = 0.7; A = 20; σ = 15
x = cumsum(randn(n)) .+ [(1 + a*i) .+ A*sin(2π/10*i) for i = 1:n] .+
[A^2*sin(2π/2*i + π) for i = 1:n] .+ σ .* rand(n).^2;
s = surrogate(x, TFTDRandomFourier(true, 0.02))
surroplot(x, s)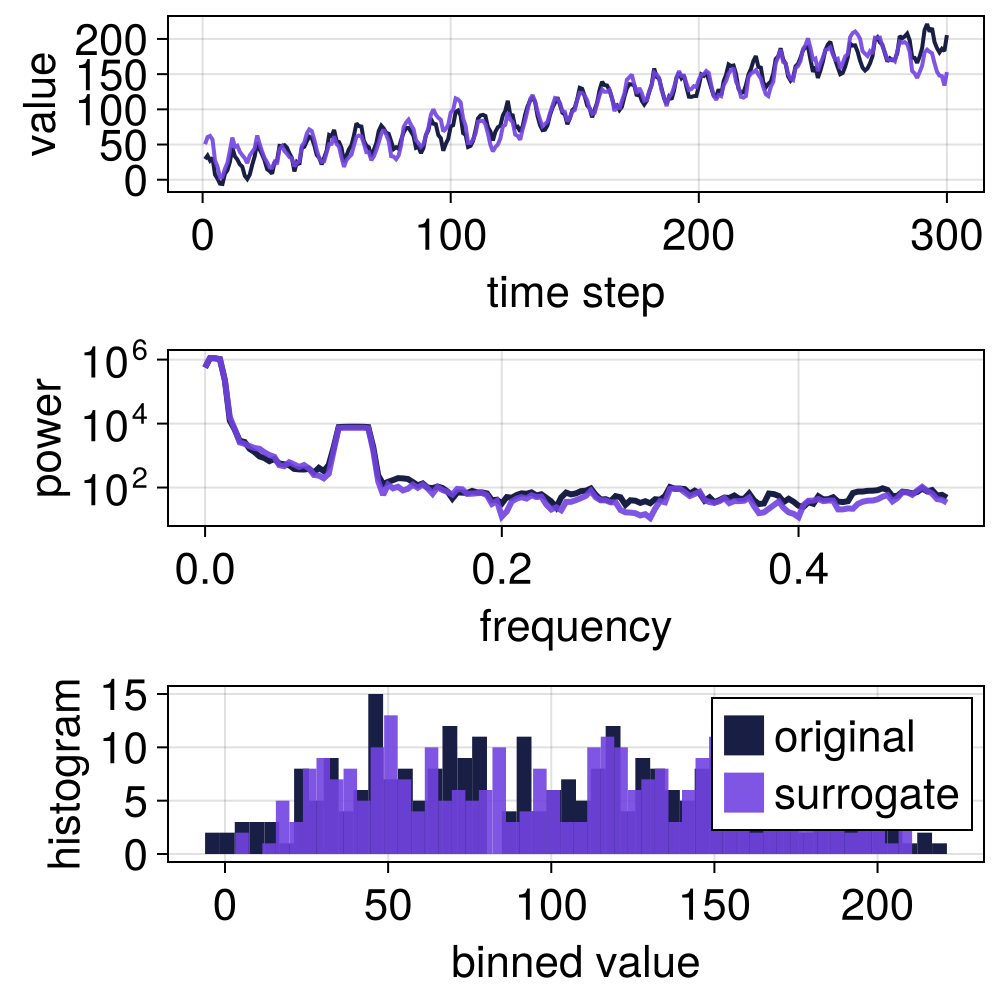
TFTDAAFT
The detrend-retrend extension of TAAFT is the TFTDAAFT method. The TFTDAAFT method adds a rescaling step to the TFTD method, ensuring that the surrogate and the original time series consist of the same values. Long-term trends in the data are also decently preserved by TFTDAAFT, but like TFTDAAFT, there is some bias.
using TimeseriesSurrogates
# Example signal
n = 300; a = 0.7; A = 20; σ = 15
x = cumsum(randn(n)) .+ [(1 + a*i) .+ A*sin(2π/10*i) for i = 1:n] .+
[A^2*sin(2π/2*i + π) for i = 1:n] .+ σ .* rand(n).^2;
# Keep 2 % of lowermost frequencies.
s = surrogate(x, TFTDAAFT(0.02))
surroplot(x, s)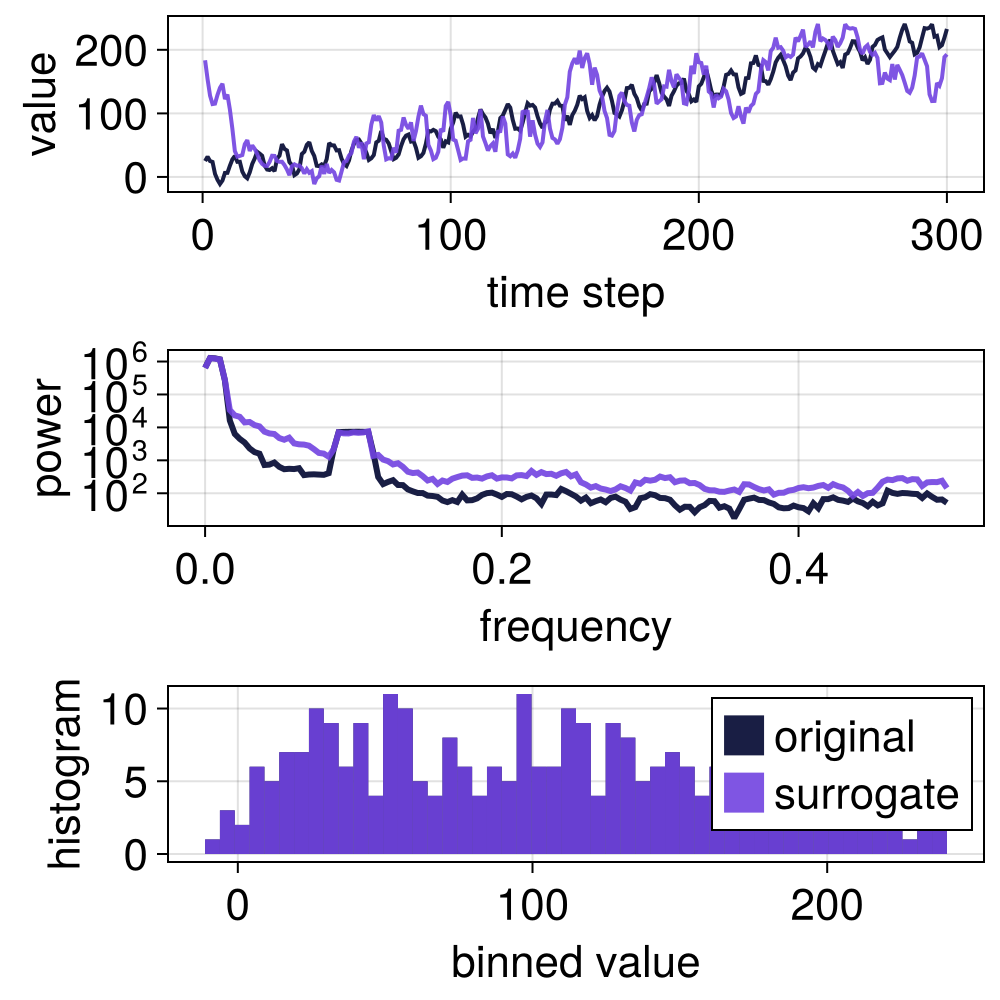
TFTDIAAFT
TFTDIAAFT[Lucio2012] surrogates are similar to TFTDAAFT surrogates, but the TFTDIAAFT[Lucio2012] method also uses an iterative process to better match the power spectra of the original signal and the surrogate (analogous to how the IAAFT method improves upon the AAFT method).
using TimeseriesSurrogates
# Example signal
n = 300; a = 0.7; A = 20; σ = 15
x = cumsum(randn(n)) .+ [(1 + a*i) .+ A*sin(2π/10*i) for i = 1:n] .+
[A^2*sin(2π/2*i + π) for i = 1:n] .+ σ .* rand(n).^2;
# Keep 5% of lowermost frequences
s = surrogate(x, TFTDIAAFT(0.05))
surroplot(x, s)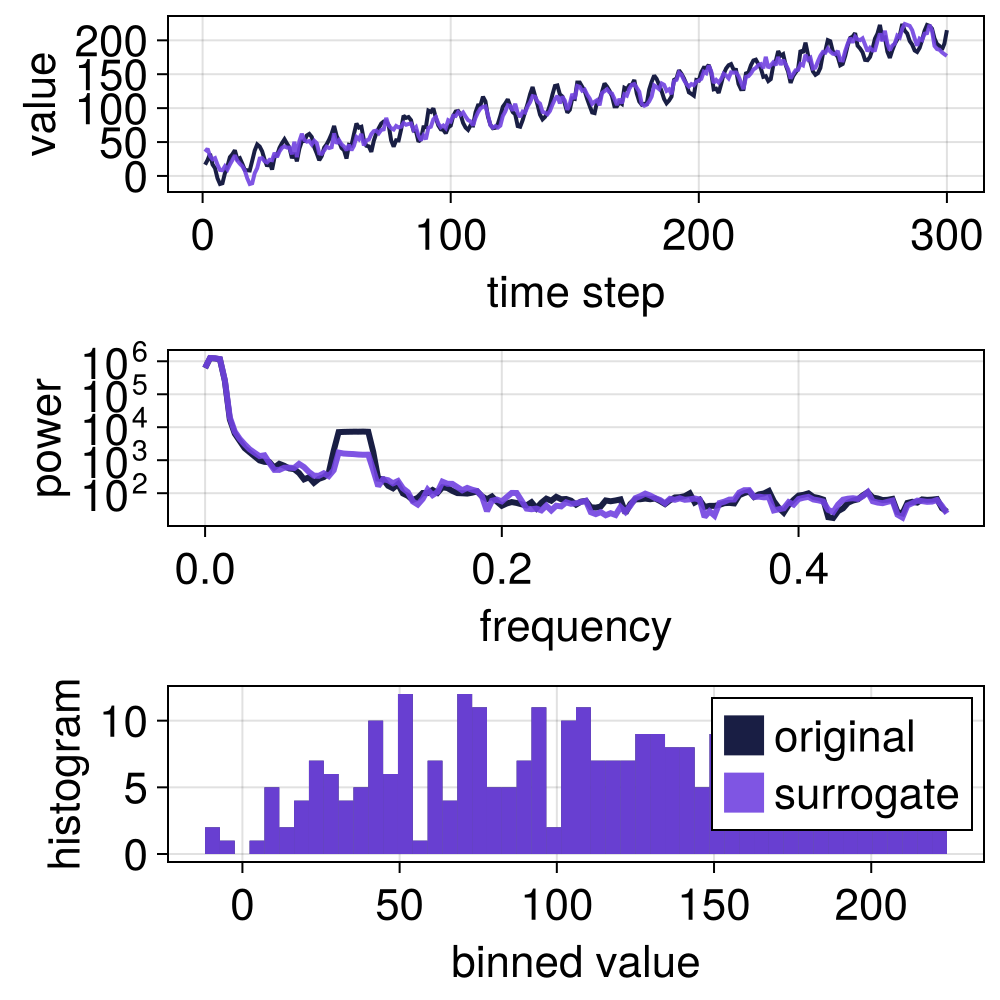
- Lucio2012Lucio, J. H., Valdés, R., & Rodríguez, L. R. (2012). Improvements to surrogate data methods for nonstationary time series. Physical Review E, 85(5), 056202.