Multidimensional surrogates
Multidimensional surrogates operate typically on input StateSpaceSets and output the same type.
Shuffle dimensions
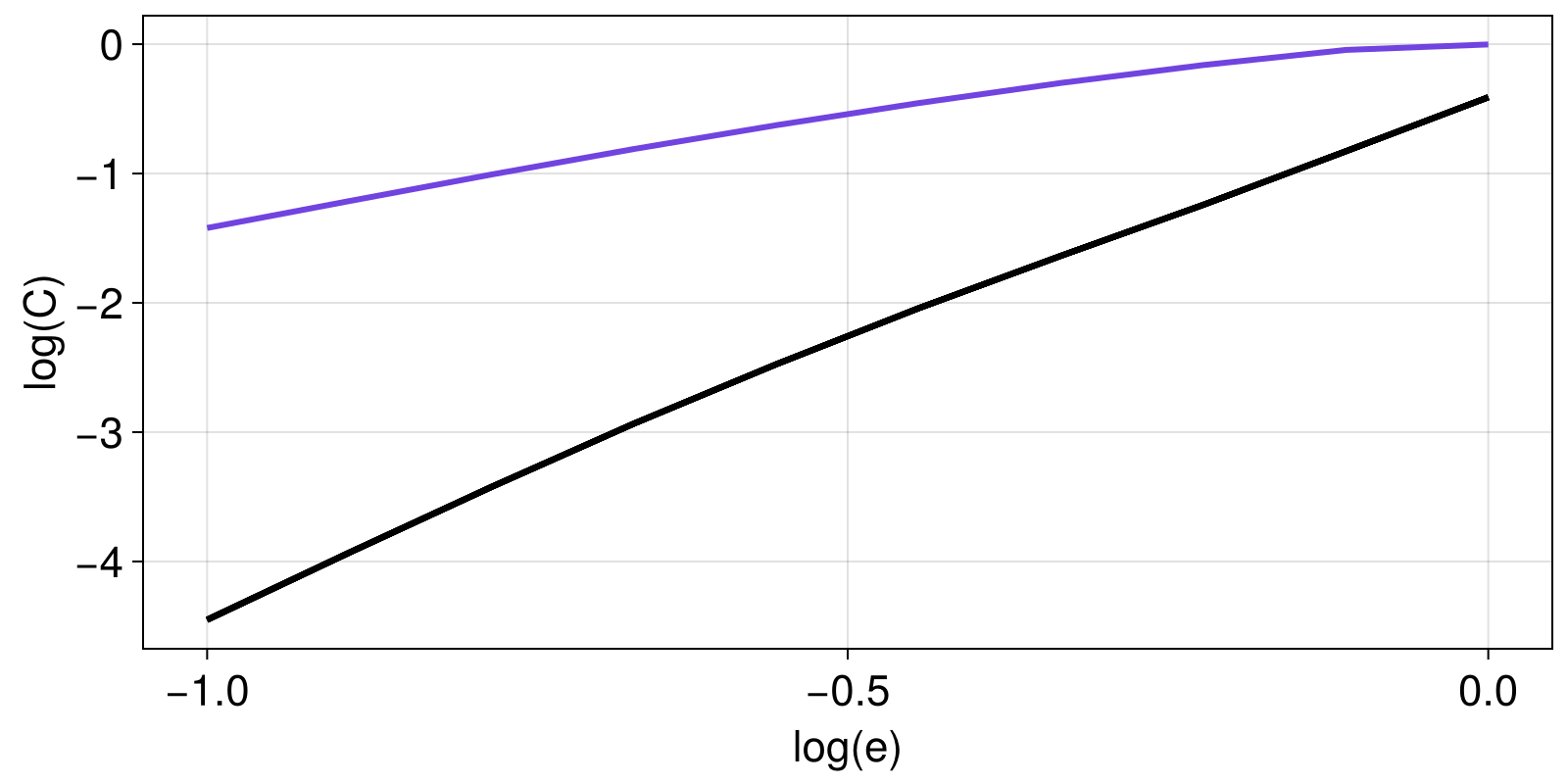
This surrogate was made to distinguish multidimensional data with structure in the state space from multidimensional noise.
Here is a simple application that shows that the distinction is successful for a system that we know a-priori is deterministic and has structure in the state space (a chaotic attractor).
using TimeseriesSurrogates
using DynamicalSystemsBase
using FractalDimensions: correlationsum
using CairoMakie
# Create a trajectory from the towel map
function towel_rule(x, p, n)
@inbounds x1, x2, x3 = x[1], x[2], x[3]
SVector( 3.8*x1*(1-x1) - 0.05*(x2+0.35)*(1-2*x3),
0.1*( (x2+0.35)*(1-2*x3) - 1 )*(1 - 1.9*x1),
3.78*x3*(1-x3)+0.2*x2 )
end
to = DeterministicIteratedMap(towel_rule, [0.1, -0.1, 0.1])
X = trajectory(to, 10_000; Ttr = 100)[1]
e = 10.0 .^ range(-1, 0; length = 10)
CX = correlationsum(X, e; w = 5)
le = log10.(e)
fig, ax = lines(le, log10.(CX))
sg = surrogenerator(X, ShuffleDimensions())
for i in 1:10
Z = sg()
CZ = correlationsum(Z, e)
lines!(ax, le, log.(CZ); color = ("black", 0.8))
end
ax.xlabel = "log(e)"; ax.ylabel = "log(C)"
fig