Wavelet surrogates

WLS

WLS surrogates are constructed by taking the maximal overlap discrete wavelet transform (MODWT) of the signal, shuffling detail coefficients across dyadic scales, then inverting the transform to obtain the surrogate.

Wavelet-IAAFT (WIAAFT) surrogates

In Keylock (2006), IAAFT shuffling is used, yielding surrogates that preserve the local mean and variance of the original signal, but randomizes nonlinear properties of the signal. This also preserves nonstationarities in the signal. To construct WIAAFT surrogates, rescaling must be enabled.

Note: the final iterative procedure of the WIAAFT surrogate method, after the rescaling step, is not performed in our current implementation, so surrogates might differ a bit from results in Keylock (2006). For now, you have to do the iterative rescaling manually if desired..

using TimeseriesSurrogates, Random
Random.seed!(5040)
n = 500
σ = 30
x = cumsum(randn(n)) .+
    [20*sin(2π/30*i) for i = 1:n] .+
    [20*cos(2π/90*i) for i = 1:n] .+
    [50*sin(2π/2*i + π) for i = 1:n] .+
    σ .* rand(n).^2 .+
    [0.5*t for t = 1:n];

# Rescale surrogate back to original values
method = WLS(IAAFT(), rescale = true)
s = surrogate(x, method);
p = surroplot(x, s)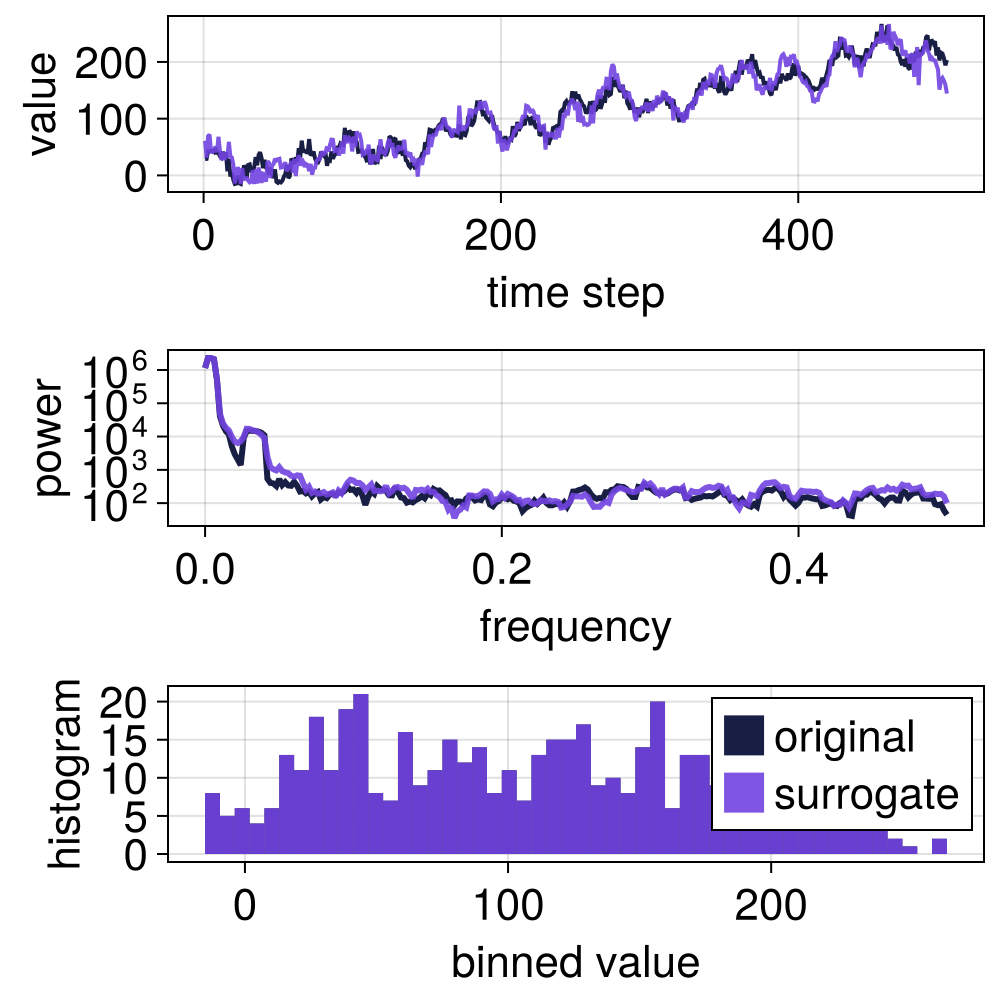

Even without rescaling, IAAFT shuffling also yields surrogates with local properties very similar to the original signal.

using TimeseriesSurrogates, Random
Random.seed!(5040)
n = 500
σ = 30
x = cumsum(randn(n)) .+
    [20*sin(2π/30*i) for i = 1:n] .+
    [20*cos(2π/90*i) for i = 1:n] .+
    [50*sin(2π/2*i + π) for i = 1:n] .+
    σ .* rand(n).^2 .+
    [0.5*t for t = 1:n];

# Don't rescale back to original time series.
method = WLS(IAAFT(), rescale = false)
s = surrogate(x, method);
p = surroplot(x, s)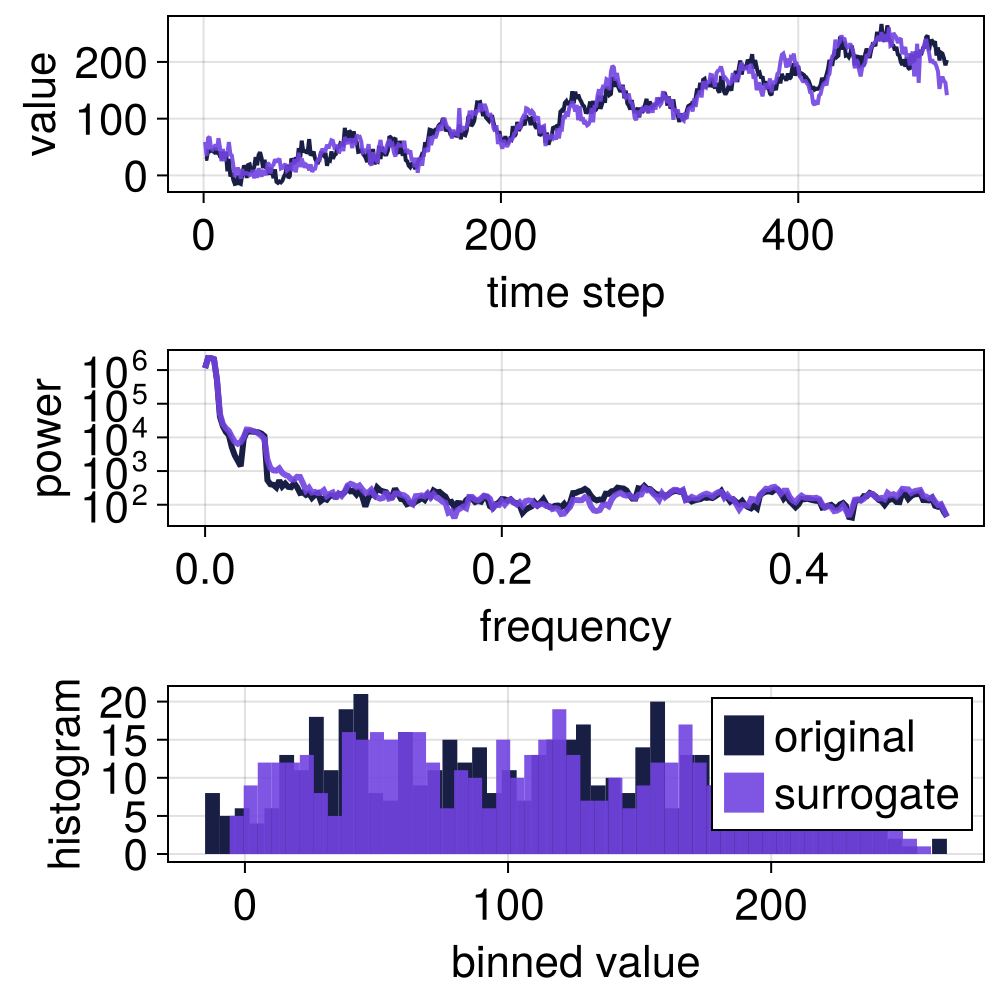

Other shuffling methods

The choice of coefficient shuffling method determines how well and which properties of the original signal are retained by the surrogates. There might be use cases where surrogates do not need to perfectly preserve the autocorrelation of the original signal, so additional shuffling methods are provided for convenience.

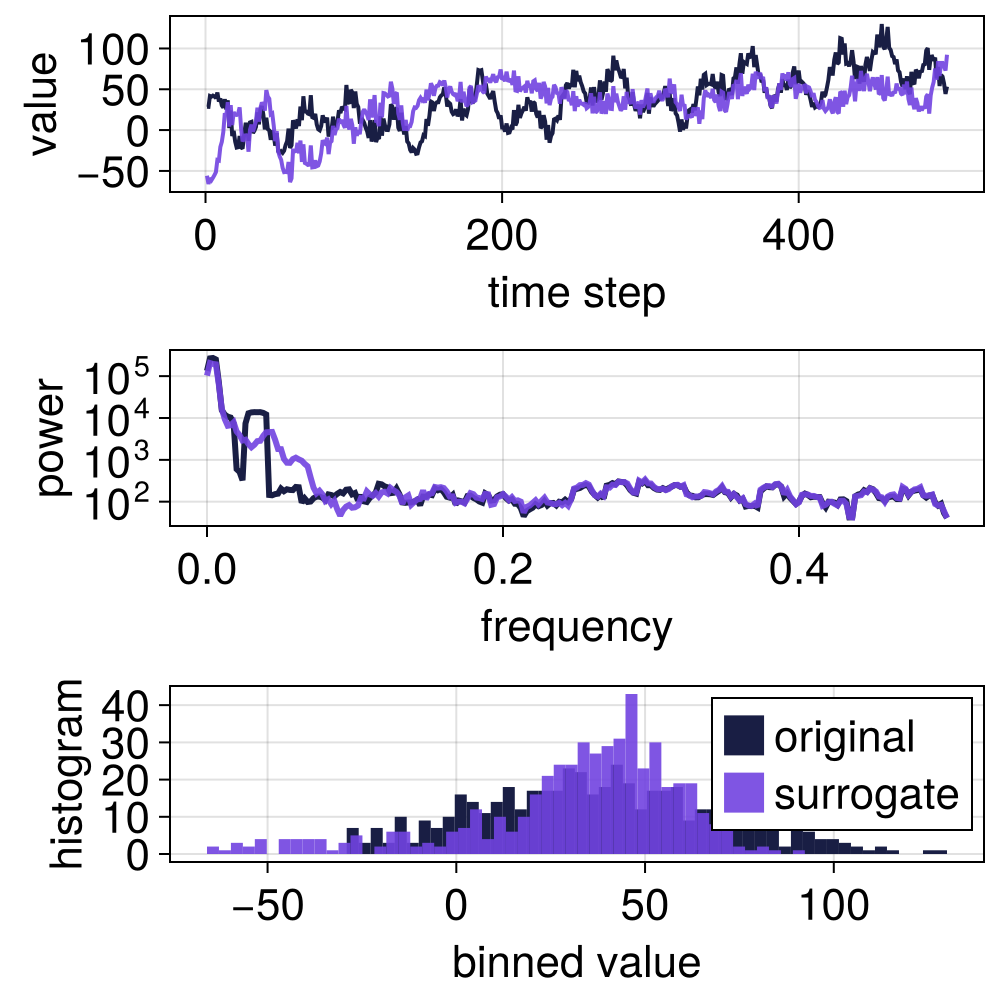
Using random shuffling of the detail coefficients does not preserve the autocorrelation structure of the original signal.

using TimeseriesSurrogates, Random
Random.seed!(5040)
n = 500
σ = 30
x = cumsum(randn(n)) .+
    [20*sin(2π/30*i) for i = 1:n] .+
    [20*cos(2π/90*i) for i = 1:n] .+
    [50*sin(2π/2*i + π) for i = 1:n] .+
    σ .* rand(n).^2 .+
    [0.5*t for t = 1:n];

method = WLS(RandomShuffle(), rescale = false)
s = surrogate(x, method);
p = surroplot(x, s)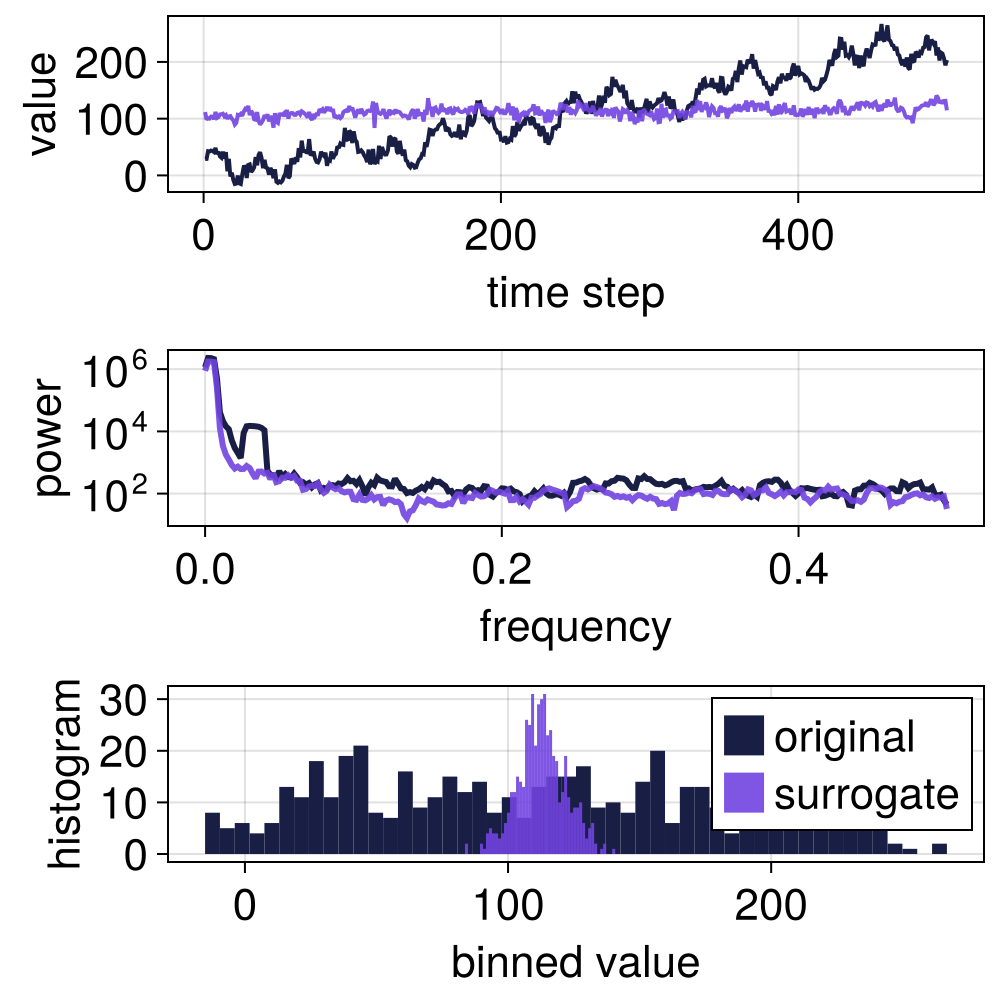

Block shuffling the detail coefficients better preserve local properties because the shuffling is not completely random, but still does not preserve the autocorrelation of the original signal.

using TimeseriesSurrogates, Random
Random.seed!(5040)
n = 500
σ = 30
x = cumsum(randn(n)) .+
    [20*sin(2π/30*i) for i = 1:n] .+
    [20*cos(2π/90*i) for i = 1:n] .+
    [50*sin(2π/2*i + π) for i = 1:n] .+
    σ .* rand(n).^2 .+
    [0.5*t for t = 1:n];

s = surrogate(x, WLS(BlockShuffle(10), rescale = false));
p = surroplot(x, s)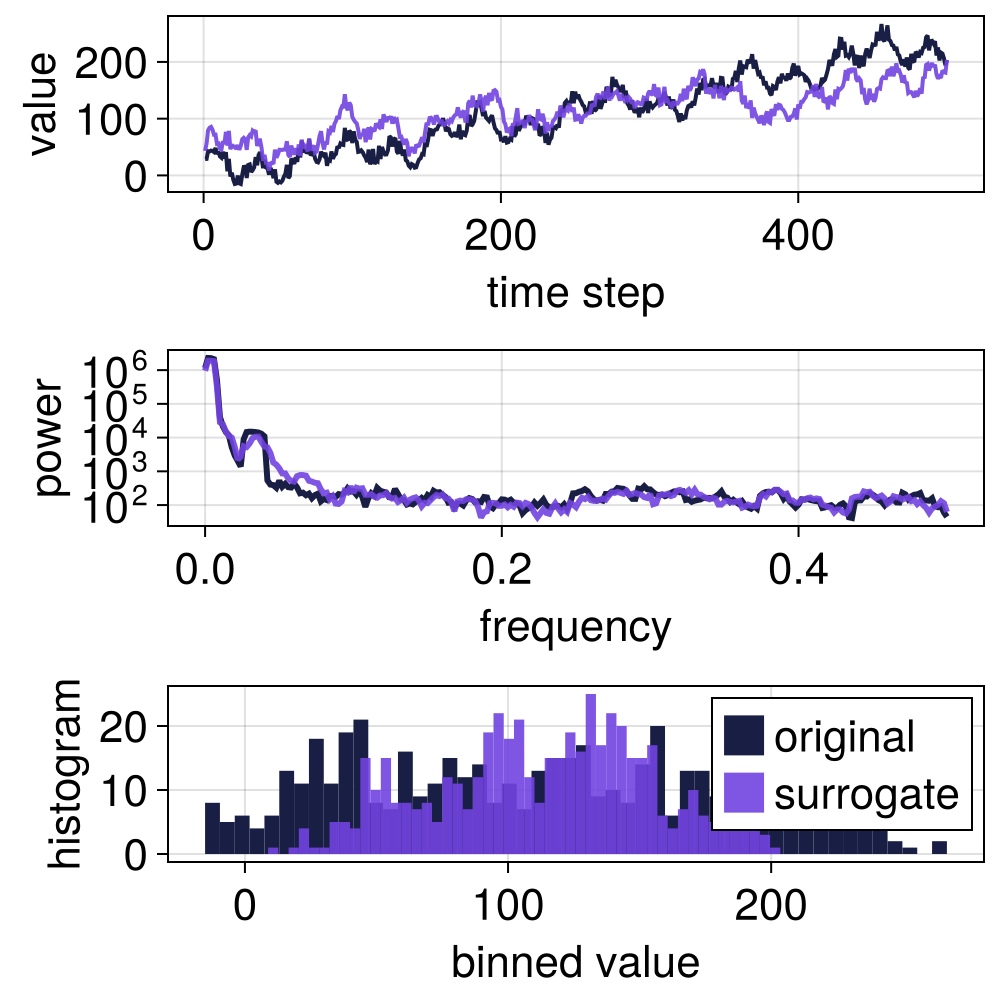

Random Fourier phase shuffling the detail coefficients does a decent job at preserving the autocorrelation.

using TimeseriesSurrogates, Random
Random.seed!(5040)
n = 500
σ = 30
x = cumsum(randn(n)) .+
    [20*sin(2π/30*i) for i = 1:n] .+
    [20*cos(2π/90*i) for i = 1:n] .+
    [50*sin(2π/2*i + π) for i = 1:n] .+
    σ .* rand(n).^2 .+
    [0.5*t for t = 1:n];

s = surrogate(x, WLS(RandomFourier(), rescale = false));
surroplot(x, s)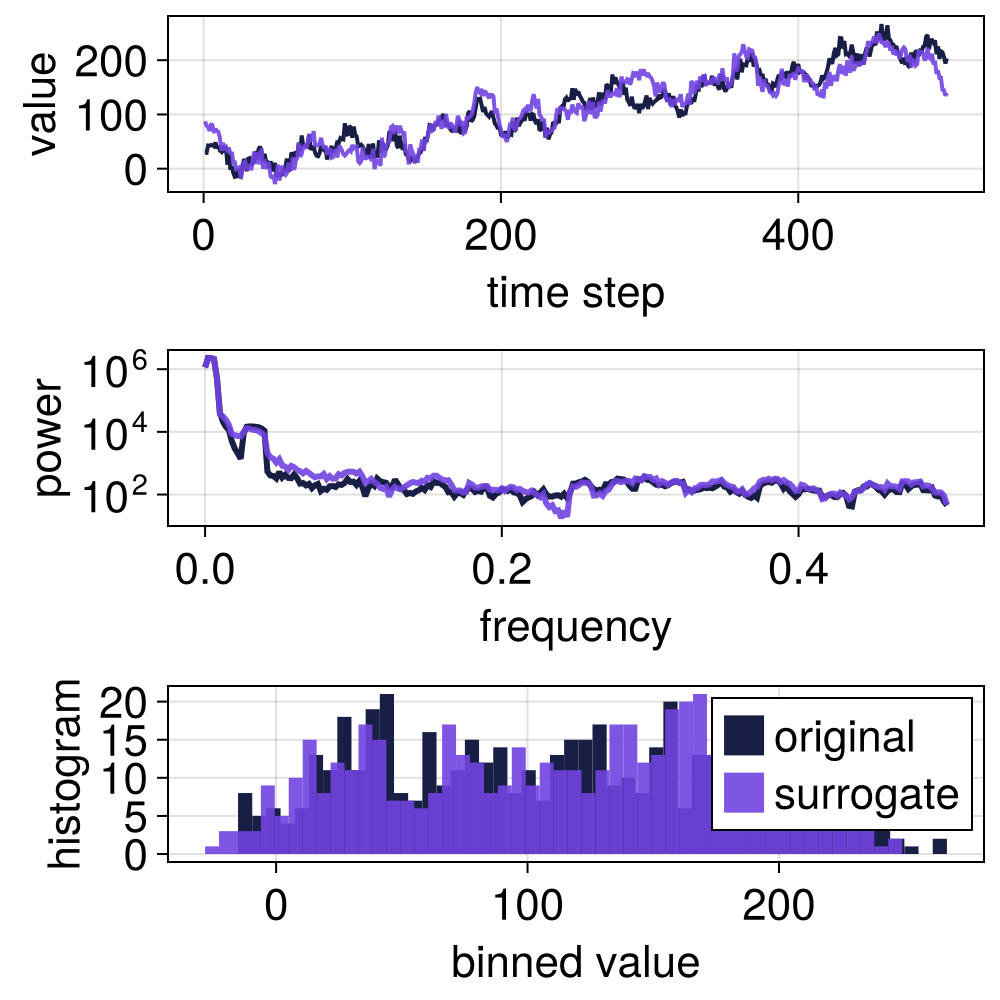

To generate surrogates that preserve linear properties of the original signal, AAFT or IAAFT shuffling is required.

RandomCascade

RandomCascade surrogates is another wavelet-based method that uses the regular discrete wavelet transform to generate surrogates.

using TimeseriesSurrogates, Random
Random.seed!(5040)
n = 500
σ = 30
x = cumsum(randn(n)) .+
     [20*sin(2π/30*i) for i = 1:n] .+
     [20*cos(2π/90*i) for i = 1:n] .+
     [50*sin(2π/2*i + π) for i = 1:n] .+
     σ .* rand(n).^2 .+
     [0.2*t for t = 1:n];

s = surrogate(x, RandomCascade());
surroplot(x, s)