Hegselmann-Krause opinion dynamics
This example showcases
- How to do synchronous updating of Agent properties (also know as Synchronous update schedule). In a Synchronous update schedule changes made to an agent are not seen by other agents until the next step, see also Wilensky 2015, p.286).
- How to terminate the system evolution on demand according to a boolean function.
- How to terminate the system evolution according to what happened on the previous step.
Model overview
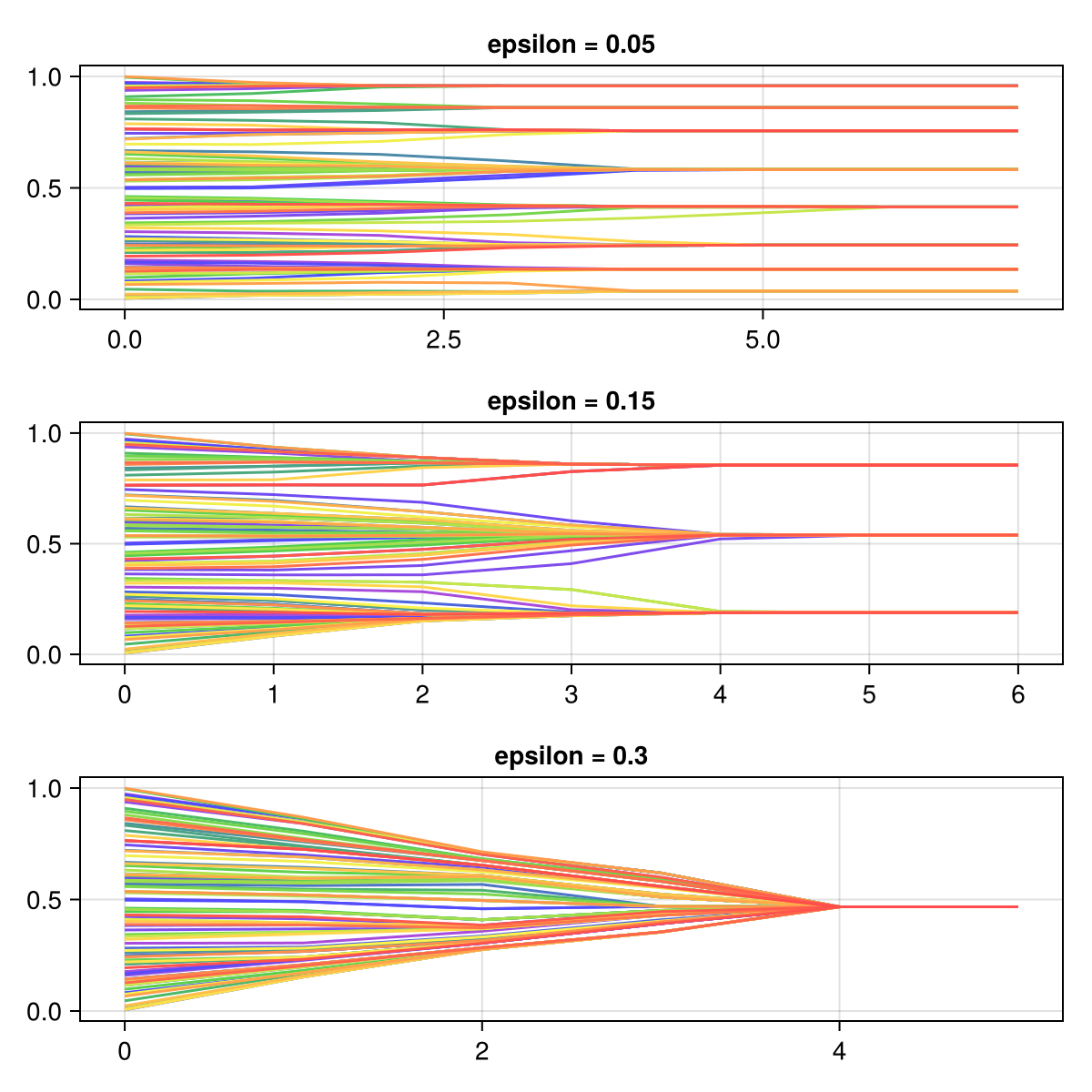
This is an implementation of a simple version of the Hegselmann and Krause (2002) model. It is a model of opinion formation with the question: which parameters' values lead to consensus, polarization or fragmentation? It models interacting groups of agents (as opposed to interacting pairs, typical in the literature) in which it is assumed that if an agent disagrees too much with the opinion of a source of influence, the source can no longer influence the agent's opinion. There is then a "bound of confidence". The model shows that the systemic configuration is heavily dependent on this parameter's value.
The model has the following components:
- A set of n Agents with opinions xᵢ in the range [0,1] as attribute
- A parameter ϵ called "bound" in (0, 0.3]
- The update rule: at each step every agent adopts the mean of the opinions which are within the confidence bound ( |xᵢ - xⱼ| ≤ ϵ).
Core structures
We start by defining the Agent type and initializing the model. The Agent type has two fields so that we can implement the synchronous update.
using Agents, Random
using Statistics: mean
@agent struct HKAgent(NoSpaceAgent)
old_opinion::Float64
new_opinion::Float64
previous_opinion::Float64
endThere is a reason the agent has three fields that are "the same". The old_opinion is used for the synchronous agent update, since we require access to a property's value at the start of the step and the end of the step. The previous_opinion is the opinion of the agent in the previous step, as the model termination requires access to a property's value at the end of the previous step, and the end of the current step.
We could, alternatively, make the three opinions a single field with vector value.
function hk_model(; numagents = 100, ϵ = 0.2)
model = StandardABM(HKAgent; agent_step!, model_step!, rng = MersenneTwister(42),
scheduler = Schedulers.fastest, properties = Dict(:ϵ => ϵ))
for i in 1:numagents
o = rand(abmrng(model))
add_agent!(model, o, o, -1)
end
return model
endhk_model (generic function with 1 method)Add some helper functions for the update rule. As there is a filter in the rule we implement it outside the agent_step! method. Notice that the filter is applied to the :old_opinion field.
function boundfilter(agent, model)
filter(
j -> abs(agent.old_opinion - j) < model.ϵ,
[a.old_opinion for a in allagents(model)],
)
endboundfilter (generic function with 1 method)Now we implement the agent_step!
function agent_step!(agent, model)
agent.previous_opinion = agent.old_opinion
agent.new_opinion = mean(boundfilter(agent, model))
endagent_step! (generic function with 1 method)and model_step!
function model_step!(model)
for a in allagents(model)
a.old_opinion = a.new_opinion
end
endmodel_step! (generic function with 1 method)From this implementation we see that to implement synchronous scheduling we define an Agent type with old and new fields for attributes that are changed via the synchronous update. In agent_step! we use the old field then, after updating all the agents new fields, we use the model_step! to update the model for the next iteration.
Running the model
The parameter of interest is now :new_opinion, so we assign it to variable adata and pass it to the run! method to be collected in a DataFrame.
In addition, we want to run the model only until all agents have converged to an opinion. From the documentation of step! one can see that instead of specifying the amount of steps we can specify a function instead.
function terminate(model, s)
if any(
!isapprox(a.previous_opinion, a.new_opinion; rtol = 1e-12)
for a in allagents(model)
)
return false
else
return true
end
end
model = hk_model()
step!(model, terminate)
model[1]Main.HKAgent(1, 0.6238087374881782, 0.6238087374881782, 0.6238087374881787)Alright, let's wrap everything in a function and do some data collection using run!.
function model_run(; kwargs...)
model = hk_model(; kwargs...)
agent_data, _ = run!(model, terminate; adata = [:new_opinion])
return agent_data
end
data = model_run(numagents = 100)
data[(end-19):end, :]| Row | time | id | new_opinion |
|---|---|---|---|
| Int64 | Int64 | Float64 | |
| 1 | 7 | 81 | 0.623809 |
| 2 | 7 | 82 | 0.623809 |
| 3 | 7 | 83 | 0.220896 |
| 4 | 7 | 84 | 0.220896 |
| 5 | 7 | 85 | 0.623809 |
| 6 | 7 | 86 | 0.623809 |
| 7 | 7 | 87 | 0.220896 |
| 8 | 7 | 88 | 0.623809 |
| 9 | 7 | 89 | 0.623809 |
| 10 | 7 | 90 | 0.220896 |
| 11 | 7 | 91 | 0.220896 |
| 12 | 7 | 92 | 0.623809 |
| 13 | 7 | 93 | 0.623809 |
| 14 | 7 | 94 | 0.623809 |
| 15 | 7 | 95 | 0.623809 |
| 16 | 7 | 96 | 0.220896 |
| 17 | 7 | 97 | 0.623809 |
| 18 | 7 | 98 | 0.623809 |
| 19 | 7 | 99 | 0.220896 |
| 20 | 7 | 100 | 0.623809 |
Notice that here we didn't speciy when to collect data, so this is done at every step. Instead, we could collect data only at the final step, by re-using the same function for the when argument:
model = hk_model()
agent_data, _ = run!(model, terminate; adata = [:new_opinion],
when = terminate)
agent_data| Row | time | id | new_opinion |
|---|---|---|---|
| Int64 | Int64 | Float64 | |
| 1 | 7 | 1 | 0.623809 |
| 2 | 7 | 2 | 0.623809 |
| 3 | 7 | 3 | 0.220896 |
| 4 | 7 | 4 | 0.220896 |
| 5 | 7 | 5 | 0.623809 |
| 6 | 7 | 6 | 0.623809 |
| 7 | 7 | 7 | 0.220896 |
| 8 | 7 | 8 | 0.220896 |
| 9 | 7 | 9 | 0.623809 |
| 10 | 7 | 10 | 0.623809 |
| 11 | 7 | 11 | 0.623809 |
| 12 | 7 | 12 | 0.220896 |
| 13 | 7 | 13 | 0.623809 |
| 14 | 7 | 14 | 0.623809 |
| 15 | 7 | 15 | 0.220896 |
| 16 | 7 | 16 | 0.623809 |
| 17 | 7 | 17 | 0.623809 |
| 18 | 7 | 18 | 0.623809 |
| 19 | 7 | 19 | 0.220896 |
| 20 | 7 | 20 | 0.623809 |
| 21 | 7 | 21 | 0.623809 |
| 22 | 7 | 22 | 0.220896 |
| 23 | 7 | 23 | 0.220896 |
| 24 | 7 | 24 | 0.623809 |
| 25 | 7 | 25 | 0.623809 |
| 26 | 7 | 26 | 0.220896 |
| 27 | 7 | 27 | 0.220896 |
| 28 | 7 | 28 | 0.623809 |
| 29 | 7 | 29 | 0.623809 |
| 30 | 7 | 30 | 0.220896 |
| 31 | 7 | 31 | 0.220896 |
| 32 | 7 | 32 | 0.220896 |
| 33 | 7 | 33 | 0.623809 |
| 34 | 7 | 34 | 0.220896 |
| 35 | 7 | 35 | 0.220896 |
| 36 | 7 | 36 | 0.623809 |
| 37 | 7 | 37 | 0.623809 |
| 38 | 7 | 38 | 0.220896 |
| 39 | 7 | 39 | 0.623809 |
| 40 | 7 | 40 | 0.623809 |
| 41 | 7 | 41 | 0.220896 |
| 42 | 7 | 42 | 0.623809 |
| 43 | 7 | 43 | 0.623809 |
| 44 | 7 | 44 | 0.220896 |
| 45 | 7 | 45 | 0.623809 |
| 46 | 7 | 46 | 0.220896 |
| 47 | 7 | 47 | 0.623809 |
| 48 | 7 | 48 | 0.623809 |
| 49 | 7 | 49 | 0.623809 |
| 50 | 7 | 50 | 0.623809 |
| 51 | 7 | 51 | 0.623809 |
| 52 | 7 | 52 | 0.220896 |
| 53 | 7 | 53 | 0.623809 |
| 54 | 7 | 54 | 0.220896 |
| 55 | 7 | 55 | 0.623809 |
| 56 | 7 | 56 | 0.220896 |
| 57 | 7 | 57 | 0.623809 |
| 58 | 7 | 58 | 0.623809 |
| 59 | 7 | 59 | 0.623809 |
| 60 | 7 | 60 | 0.623809 |
| 61 | 7 | 61 | 0.623809 |
| 62 | 7 | 62 | 0.623809 |
| 63 | 7 | 63 | 0.623809 |
| 64 | 7 | 64 | 0.623809 |
| 65 | 7 | 65 | 0.623809 |
| 66 | 7 | 66 | 0.220896 |
| 67 | 7 | 67 | 0.220896 |
| 68 | 7 | 68 | 0.220896 |
| 69 | 7 | 69 | 0.623809 |
| 70 | 7 | 70 | 0.623809 |
| 71 | 7 | 71 | 0.220896 |
| 72 | 7 | 72 | 0.623809 |
| 73 | 7 | 73 | 0.623809 |
| 74 | 7 | 74 | 0.220896 |
| 75 | 7 | 75 | 0.220896 |
| 76 | 7 | 76 | 0.623809 |
| 77 | 7 | 77 | 0.220896 |
| 78 | 7 | 78 | 0.220896 |
| 79 | 7 | 79 | 0.220896 |
| 80 | 7 | 80 | 0.623809 |
| 81 | 7 | 81 | 0.623809 |
| 82 | 7 | 82 | 0.623809 |
| 83 | 7 | 83 | 0.220896 |
| 84 | 7 | 84 | 0.220896 |
| 85 | 7 | 85 | 0.623809 |
| 86 | 7 | 86 | 0.623809 |
| 87 | 7 | 87 | 0.220896 |
| 88 | 7 | 88 | 0.623809 |
| 89 | 7 | 89 | 0.623809 |
| 90 | 7 | 90 | 0.220896 |
| 91 | 7 | 91 | 0.220896 |
| 92 | 7 | 92 | 0.623809 |
| 93 | 7 | 93 | 0.623809 |
| 94 | 7 | 94 | 0.623809 |
| 95 | 7 | 95 | 0.623809 |
| 96 | 7 | 96 | 0.220896 |
| 97 | 7 | 97 | 0.623809 |
| 98 | 7 | 98 | 0.623809 |
| 99 | 7 | 99 | 0.220896 |
| 100 | 7 | 100 | 0.623809 |
Finally we run three scenarios, collect the data and plot it.
using DataFrames, CairoMakie
const cmap = cgrad(:lightrainbow)
plotsim(ax, data) =
for grp in groupby(data, :id)
lines!(ax, grp.time, grp.new_opinion, color = cmap[grp.id[1]/100])
end
eps = [0.05, 0.15, 0.3]
figure = Figure(size = (600, 600))
for (i, e) in enumerate(eps)
ax = figure[i, 1] = Axis(figure; title = "epsilon = $e")
e_data = model_run(ϵ = e)
plotsim(ax, e_data)
end
figure