Opinion spread

This is a simple model of how an opinion spreads through a community. Each individual has a number of opinions as a list of integers. They can change their opinion by changing the numbers in the list.

Agents can change their opinion at each step. They choose one of their neighbors Randomly(), and adopt one of the neighbor's opinions. They are more likely to adopt their neighbor's opinion if they share more opinions with each other.

Notice that just like the Forest fire and Conway's game of life examples this model is a Cellular Automaton: one agent exists per position and agents never move, or are killed/added after model creation. This means that a much more performant version can be done without any agents, but just matrices representing spatial properties just like in Conway's game of life. However, some users may find more this agent-based formulation more intuitive, and hence this example follows this approach.

using Agents
using CairoMakie # for static plotting
using Random
using StatsBase

Model creation

@agent struct Citizen(GridAgent{2})
    stabilized::Bool
    opinion::Array{Int,1}
    prev_opinion::Array{Int,1}
end

function create_model(; dims = (10, 10), nopinions = 3, levels_per_opinion = 4, seed = 648)
    space = GridSpace(dims)
    properties = Dict(:nopinions => nopinions)
    model = StandardABM(
        Citizen,
        space;
        agent_step!,
        scheduler = Schedulers.Randomly(),
        properties = properties,
        rng = MersenneTwister(seed),
    )
    for pos in positions(model)
        opinion = sample(abmrng(model), 1:levels_per_opinion, nopinions, replace = false)
        prev_opinion = sample(abmrng(model), 1:levels_per_opinion, nopinions, replace = false)
        add_agent!(pos, model, false, opinion, prev_opinion)
    end
    return model
end

create_model (generic function with 1 method)

Stepping functions

function agent_step!(agent, model)
    update_prev_opinion!(agent, model)
    adopt!(agent, model)
    stabilize!(agent)
end

function update_prev_opinion!(agent, model)
    for i in 1:(model.nopinions)
        agent.prev_opinion[i] = agent.opinion[i]
    end
end

function adopt!(agent, model)
    neighbor = sample(abmrng(model), collect(nearby_ids(agent, model))) # Randomly select a neighbor.
    neighbor_opinions = model[neighbor].opinion # Look up neighbor's opinions.
    agent_opinions = agent.opinion # Look up agent's opinions.
    nmatches = length(intersect(neighbor_opinions, agent_opinions)) # Count how many opinions the neighbor and agent have in common.

    if nmatches < model.nopinions && rand(abmrng(model)) < nmatches / model.nopinions
        neighbor_opinion = sample(abmrng(model), setdiff(neighbor_opinions, agent_opinions)) # Find which opinions the neighbor has that the agent doesn't and Randomly() pick one for the agent to adopt.
        agent_opinion = sample(abmrng(model), setdiff(agent_opinions, neighbor_opinions)) # Find which opinions the agent has that the neighbour doesn't and Randomly() pick one to change.
        replace!(agent.opinion, agent_opinion => neighbor_opinion) # Replace agent's opinion with neighbor's opinion.
    end
end

function stabilize!(agent)
    if agent.prev_opinion == agent.opinion
        agent.stabilized = true
    else
        agent.stabilized = false
    end
end

stabilize! (generic function with 1 method)

Running the model

First, we create a stopping condition, which runs the model until all agents stabilize.

rununtil(model, s) = count(a -> a.stabilized, allagents(model)) == length(positions(model))

rununtil (generic function with 1 method)

Then we create our model, run it and collect some information

model = create_model(nopinions = 3, levels_per_opinion = 4)

agentdata, _ = run!(model, rununtil, adata = [(:stabilized, count)])

(99×2 DataFrame
 Row │ time   count_stabilized
     │ Int64  Int64
─────┼─────────────────────────
   1 │     0                 0
   2 │     1                54
   3 │     2                59
   4 │     3                63
   5 │     4                57
   6 │     5                54
   7 │     6                62
   8 │     7                70
  ⋮  │   ⋮           ⋮
  93 │    92                98
  94 │    93                96
  95 │    94                95
  96 │    95                98
  97 │    96                98
  98 │    97                99
  99 │    98               100
                84 rows omitted, 0×0 DataFrame)

Plotting

The plot shows the number of stable agents, that is, number of agents whose opinions don't change from one step to the next. Note that the number of stable agents can fluctuate before the final convergence.

f = Figure(resolution = (600, 400))
ax =
    f[1, 1] = Axis(
        f,
        xlabel = "Generation",
        ylabel = "# of stabilized agents",
        title = "Population Stability",
    )
lines!(ax, 1:size(agentdata, 1), agentdata.count_stabilized, linewidth = 2, color = :blue)
f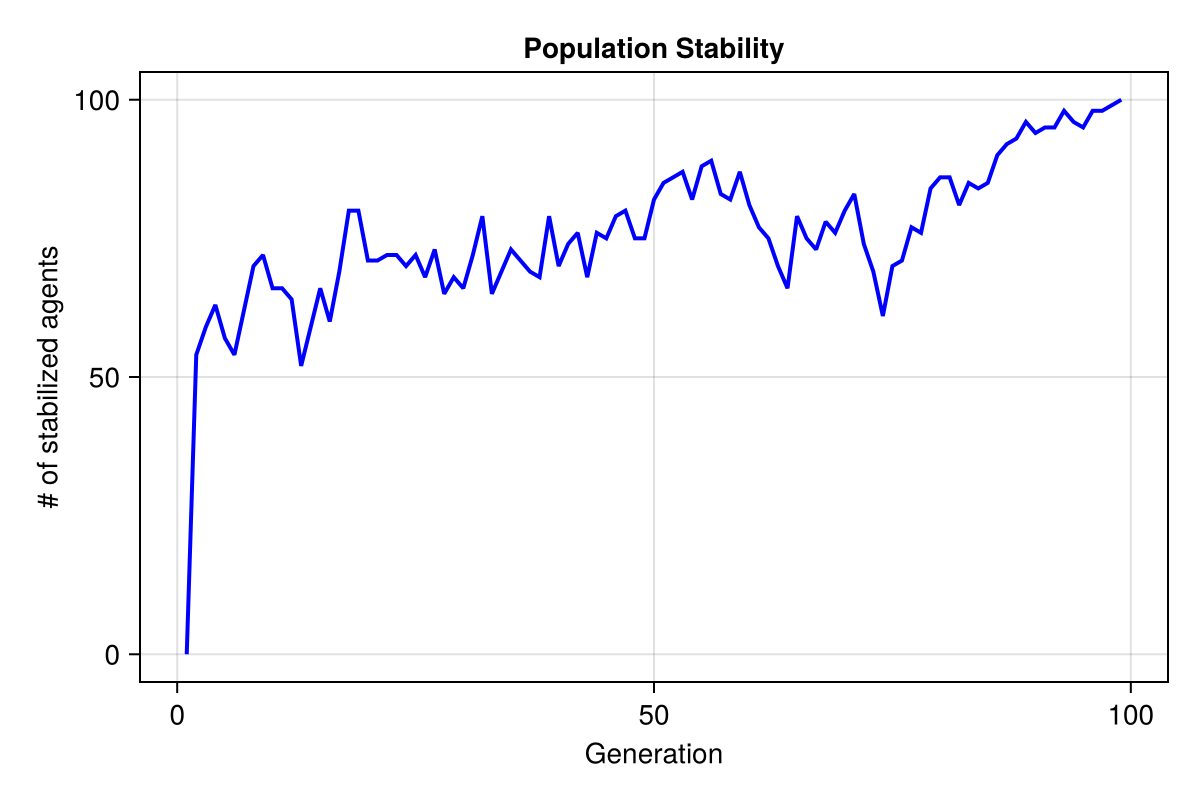

Animation

Here is an animation that shows the stabilization of agent opinions over time.

ac(agent) = agent.stabilized == true ? :purple : :green
model = create_model(nopinions = 3, levels_per_opinion = 4)

abmvideo(
    "opinion.mp4",
    model;
    agent_color = ac,
    agent_marker = '■',
    agent_size = 20,
    framerate = 20,
    frames = 60,
    title = "Opinion Spread",
)