SIR model for the spread of COVID-19
This example illustrates how to use GraphSpace and how to model agents on an graph (network) where the transition probabilities between each node (position) is not constant.
SIR model
A SIR model tracks the ratio of Susceptible, Infected, and Recovered individuals within a population. Here we add one more category of individuals: those who are infected, but do not know it. Transmission rate for infected and diagnosed individuals is lower than infected and undetected. We also allow a fraction of recovered individuals to catch the disease again, meaning that recovering the disease does not bring full immunity.
Model parameters
Here are the model parameters, some of which have default values.
Ns: a vector of population sizes per city. The amount of cities is justC=length(Ns).β_und: a vector for transmission probabilities β of the infected but undetected per city. Transmission probability is how many susceptible are infected per day by an infected individual. If social distancing is practiced, this number decreases.β_det: an array for transmission probabilities β of the infected and detected per city. If hospitals are full, this number increases.infection_period = 30: how many days before a person dies or recovers.detection_time = 14: how many days before an infected person is detected.death_rate = 0.02: the probability that the individual will die after theinfection_period.reinfection_probability = 0.05: The probability that a recovered person can get infected again.migration_rates: A matrix of migration probability per individual per day from one city to another.Is = [zeros(C-1)..., 1]: An array for initial number of infected but undetected people per city. This starts as only one infected individual in the last city.
Notice that Ns, β, Is all need to have the same length, as they are numbers for each city. We've tried to add values to the infection parameters similar to the ones you would hear on the news about COVID-19.
The good thing with Agent based models is that you could easily extend the model we implement here to also include age as an additional property of each agent. This makes ABMs flexible and suitable for research of virus spreading.
Making the model in Agents.jl
We start by defining the PoorSoul agent type and the ABM
using Agents, Random
using Agents.DataFrames, Agents.Graphs
using StatsBase: sample, Weights
using DrWatson: @dict
using CairoMakie
@agent struct PoorSoul(GraphAgent)
days_infected::Int # number of days since is infected
status::Symbol # 1: S, 2: I, 3:R
end
function model_initiation(;
Ns,
migration_rates,
β_und,
β_det,
infection_period = 30,
reinfection_probability = 0.05,
detection_time = 14,
death_rate = 0.02,
Is = [zeros(Int, length(Ns) - 1)..., 1],
seed = 0,
)
rng = Xoshiro(seed)
@assert length(Ns) ==
length(Is) ==
length(β_und) ==
length(β_det) ==
size(migration_rates, 1) "length of Ns, Is, and B, and number of rows/columns in migration_rates should be the same "
@assert size(migration_rates, 1) == size(migration_rates, 2) "migration_rates rates should be a square matrix"
C = length(Ns)
# normalize migration_rates
migration_rates_sum = sum(migration_rates, dims = 2)
for c in 1:C
migration_rates[c, :] ./= migration_rates_sum[c]
end
properties = @dict(
Ns,
Is,
β_und,
β_det,
β_det,
migration_rates,
infection_period,
infection_period,
reinfection_probability,
detection_time,
C,
death_rate,
)
space = GraphSpace(complete_graph(C))
model = StandardABM(PoorSoul, space; agent_step!, properties, rng)
# Add initial individuals
for city in 1:C, n in 1:Ns[city]
ind = add_agent!(city, model, 0, :S) # Susceptible
end
# add infected individuals
for city in 1:C
inds = ids_in_position(city, model)
for n in 1:Is[city]
agent = model[inds[n]]
agent.status = :I # Infected
agent.days_infected = 1
end
end
return model
endmodel_initiation (generic function with 1 method)We will make a function that starts a model with C number of cities, and creates the other parameters automatically by attributing some random values to them. You could directly use the above constructor and specify all Ns, β, etc. for a given set of cities.
All cities are connected with each other, while it is more probable to travel from a city with small population into a city with large population.
using LinearAlgebra: diagind
function create_params(;
C,
max_travel_rate,
infection_period = 30,
reinfection_probability = 0.05,
detection_time = 14,
death_rate = 0.02,
Is = [zeros(Int, C - 1)..., 1],
seed = 19,
)
Random.seed!(seed)
Ns = rand(50:5000, C)
β_und = rand(0.3:0.02:0.6, C)
β_det = β_und ./ 10
Random.seed!(seed)
migration_rates = zeros(C, C)
for c in 1:C
for c2 in 1:C
migration_rates[c, c2] = (Ns[c] + Ns[c2]) / Ns[c]
end
end
maxM = maximum(migration_rates)
migration_rates = (migration_rates .* max_travel_rate) ./ maxM
migration_rates[diagind(migration_rates)] .= 1.0
params = @dict(
Ns,
β_und,
β_det,
migration_rates,
infection_period,
reinfection_probability,
detection_time,
death_rate,
Is
)
return params
endcreate_params (generic function with 1 method)SIR Stepping functions
Now we define the functions for modelling the virus spread in time
function agent_step!(agent, model)
migrate!(agent, model)
transmit!(agent, model)
update!(agent, model)
recover_or_die!(agent, model)
end
function migrate!(agent, model)
pid = agent.pos
m = sample(abmrng(model), 1:(model.C), Weights(model.migration_rates[pid, :]))
if m ≠ pid
move_agent!(agent, m, model)
end
end
function transmit!(agent, model)
agent.status == :S && return
rate = if agent.days_infected < model.detection_time
model.β_und[agent.pos]
else
model.β_det[agent.pos]
end
n = rate * abs(randn(abmrng(model)))
n <= 0 && return
for contactID in ids_in_position(agent, model)
contact = model[contactID]
if contact.status == :S ||
(contact.status == :R && rand(abmrng(model)) ≤ model.reinfection_probability)
contact.status = :I
n -= 1
n <= 0 && return
end
end
end
update!(agent, model) = agent.status == :I && (agent.days_infected += 1)
function recover_or_die!(agent, model)
if agent.days_infected ≥ model.infection_period
if rand(abmrng(model)) ≤ model.death_rate
remove_agent!(agent, model)
else
agent.status = :R
agent.days_infected = 0
end
end
end
params = create_params(C = 8, max_travel_rate = 0.01)
model = model_initiation(; params...)StandardABM with 28540 agents of type PoorSoul
agents container: Dict
space: GraphSpace with 8 positions and 28 edges
scheduler: fastest
properties: Is, death_rate, infection_period, β_und, Ns, migration_rates, detection_time, reinfection_probability, β_det, CExample animation
At the moment abmplot does not plot GraphSpaces, but we can still utilize the ABMObservable. We do not need to collect data here, only the current status of the model will be used in visualization
using CairoMakie
abmobs = ABMObservable(model)ABMObservable with model:
StandardABM with 28540 agents of type PoorSoul
agents container: Dict
space: GraphSpace with 8 positions and 28 edges
scheduler: fastest
properties: Is, death_rate, infection_period, β_und, Ns, migration_rates, detection_time, reinfection_probability, β_det, C
and with data collection:
adata: nothing
mdata: nothingWe then initialize elements that are lifted observables from abmobs:
infected_fraction(m, x) = count(m[id].status == :I for id in x) / length(x)
infected_fractions(m) = [infected_fraction(m, ids_in_position(p, m)) for p in positions(m)]
fracs = lift(infected_fractions, abmobs.model)
color = lift(fs -> [cgrad(:inferno)[f] for f in fs], fracs)
title = lift(
(m) -> "step = $(abmtime(m)), infected = $(round(Int, 100*infected_fraction(m, allids(m))))%",
abmobs.model
)Observable("step = 0, infected = 0%")
And lastly we use them to plot things in a figure
fig = Figure(size = (600, 400))
ax = Axis(fig[1, 1]; title, xlabel = "City", ylabel = "Population")
barplot!(ax, model.Ns; strokecolor = :black, strokewidth = 1, color)
fig
Now we can even make an animation of it
record(fig, "covid_evolution.mp4"; framerate = 5) do io
for j in 1:30
recordframe!(io)
Agents.step!(abmobs, 1)
end
recordframe!(io)
end"covid_evolution.mp4"One can really see "explosive growth" in this animation. Things look quite calm for a while and then suddenly supermarkets have no toilet paper anymore!
Exponential growth
We now run the model and collect data. We define two useful functions for data collection:
infected(x) = count(i == :I for i in x)
recovered(x) = count(i == :R for i in x)and then collect data
model = model_initiation(; params...)
to_collect = [(:status, f) for f in (infected, recovered, length)]
data, _ = run!(model, 100; adata = to_collect)
data[1:10, :]| Row | time | infected_status | recovered_status | length_status |
|---|---|---|---|---|
| Int64 | Int64 | Int64 | Int64 | |
| 1 | 0 | 1 | 0 | 28540 |
| 2 | 1 | 2 | 0 | 28540 |
| 3 | 2 | 4 | 0 | 28540 |
| 4 | 3 | 10 | 0 | 28540 |
| 5 | 4 | 32 | 0 | 28540 |
| 6 | 5 | 98 | 0 | 28540 |
| 7 | 6 | 281 | 0 | 28540 |
| 8 | 7 | 829 | 0 | 28540 |
| 9 | 8 | 2392 | 0 | 28540 |
| 10 | 9 | 4349 | 0 | 28540 |
We now plot how quantities evolved in time to show the exponential growth of the virus
N = sum(model.Ns) # Total initial population
fig = Figure(size = (600, 400))
ax = fig[1, 1] = Axis(fig, xlabel = "steps", ylabel = "log10(count)")
li = lines!(ax, data.time, log10.(data[:, dataname((:status, infected))]), color = :blue)
lr = lines!(ax, data.time, log10.(data[:, dataname((:status, recovered))]), color = :red)
dead = log10.(N .- data[:, dataname((:status, length))])
ld = lines!(ax, data.time, dead, color = :green)
Legend(fig[1, 2], [li, lr, ld], ["infected", "recovered", "dead"])
fig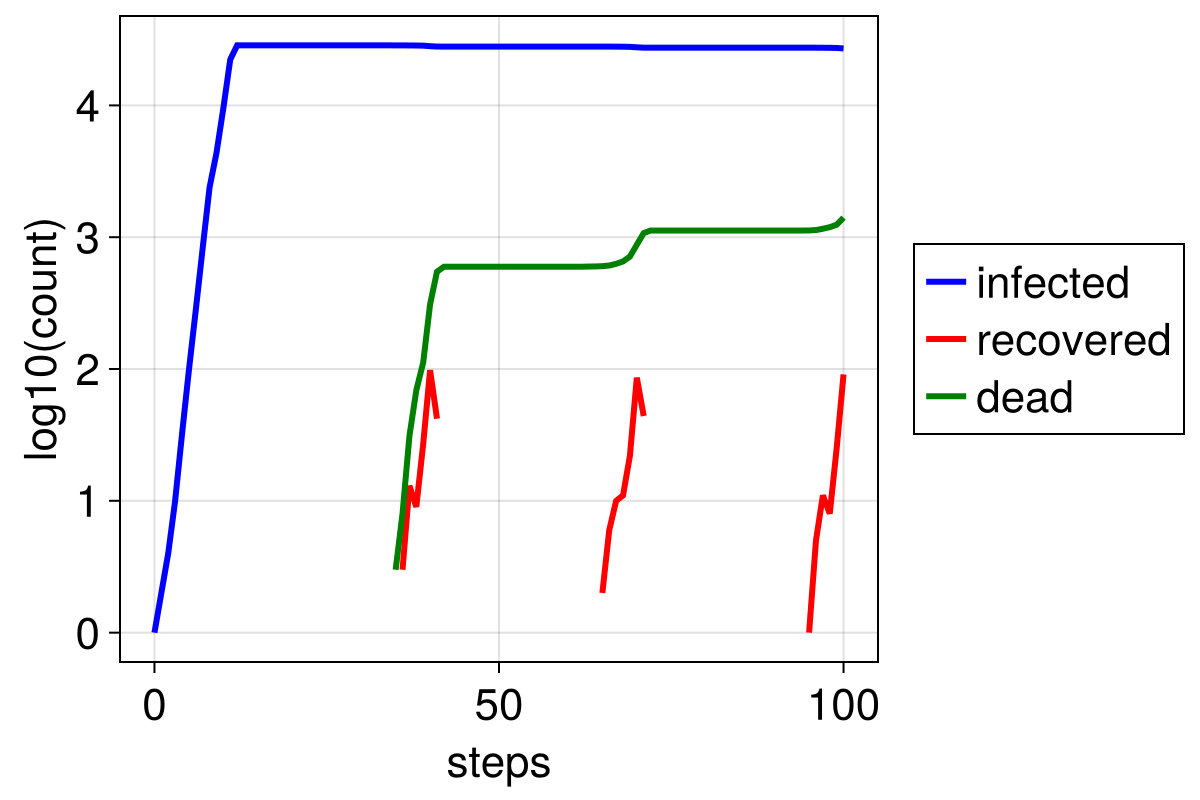
The exponential growth is clearly visible since the logarithm of the number of infected increases linearly, until everyone is infected.